Freundlich Isotherm
Freundlich Isotherm is an adsorption isotherm that describes the relationship between the concentration of a solute in a solution and its adsorption onto a solid surface. It is commonly used in chemistry and environmental science to study adsorption processes. It is manifested by an empirical equation that provides insights into the behavior of solutes on solid surfaces. [1-3]
The Freundlich Isotherm helps understand surface area, temperature, pressure, and concentration influencing adsorption processes. It also aids scientists and engineers in designing efficient materials and processes for diverse applications ranging from water purification to gas separation.
The model is named after German chemist Herbert Freundlich, who expressed it in 1909.
Equation
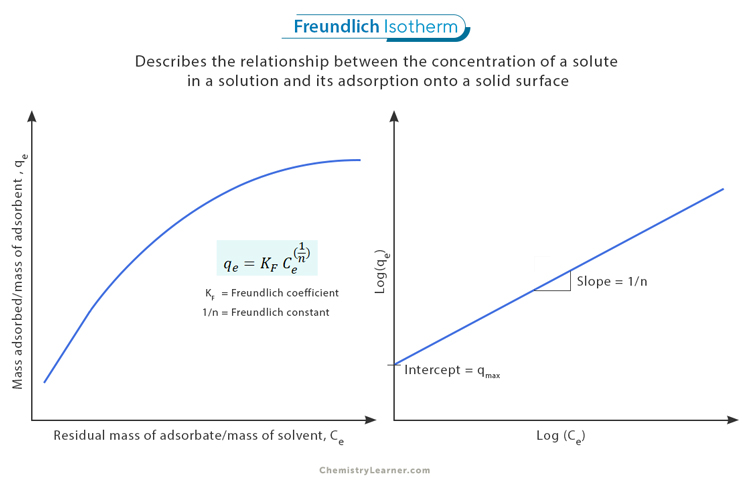
The Freundlich Isotherm equation is expressed as: [1-4]
qe = KF * Ce^(1/n)
Where:
- qe represents the mass adsorbed per unit mass of adsorbent (adsorption capacity)
- KF is a constant related to the adsorption capacity, known as the Freundlich coefficient
- Ce represents the equilibrium concentration of the adsorbate in solution
- n is another constant associated with the intensity of adsorption, known as the Freundlich constant. Typically, 0.7 < 1/n < 1.0.
In the case of gas adsorption, C is replaced by the pressure P.
The Freundlich equation suggests that as the concentration of an adsorbate increases, so does its adsorption capacity on a solid surface. However, it also implies that there may be diminishing returns with higher concentrations, as indicated by the exponent 1/n.
The constants KF and n are empirical parameters that must be determined experimentally for each specific system. They can vary depending on temperature, pressure, and properties of both the adsorbent and adsorbate.
Interpreting the Freundlich Isotherm Graph
Interpreting the Freundlich isotherm graph involves understanding the relationship between the adsorbed amount of a substance and its concentration. One key characteristic of the Freundlich isotherm graph is that it exhibits a linear relationship when plotted on logarithmic scales. Specifically, when the logarithm of the adsorbed amount (log(qe)) is plotted against the logarithm of the concentration (log(Ce)), a straight line is obtained. [1]
The value of 1/n can be between 0 and 1; therefore, the equation holds good only over a limited concentration range.
- When 1/n = 0, qe is constant, th adsorption is independent of concentration.
- When 1/n =1, qe = KF * Ce, adsorption is directly proportional to concentration.
The intercept on the y-axis (qmax) provides insights into the maximum amount of substance that can be adsorbed at saturation. This value represents an equilibrium point where a further increase in concentration does not result in additional adsorption.
Limitations of the Freundlich Isotherm Model
One of the main limitations of the Freundlich Isotherm equation lies in its assumptions. The model assumes a homogeneous distribution of active sites on the adsorbent surface, and each site has an equal affinity for the adsorbate. This assumption may only hold for some systems, especially when dealing with complex surfaces or heterogeneous materials. [1]
Another limitation is that the Freundlich model does not account for any interactions between adsorbate molecules on the surface. It assumes that each molecule adsorbs independently, which may not accurately represent real-world scenarios where interactions between molecules can affect their adsorption behavior.
Additionally, while the Freundlich equation has been successfully applied to many systems and adsorbates, its applicability can be limited to specific ranges of concentrations or temperatures. It may not accurately describe adsorption behavior at very low or high concentrations or under extreme temperature conditions.
References