English scientist Michael Faraday formulated two fundamental laws in 1833 that govern the process of electrolysis. These laws, known as Faraday’s Laws of Electrolysis, are crucial in understanding the relationship between the amount of substance produced or consumed during electrolysis and the electric charge passed through the electrolyte. ^[1-4]

Faraday’s First Law

Faraday’s First Law states that the amount of a substance produced during electrolysis is directly proportional to the quantity of electric charge passed through the electrolyte. This law dictates that the mass of a substance deposited or liberated at an electrode during electrolysis is directly proportional to the amount of electricity passed through the electrolyte. ^[1-4]

Formula

Mathematically, Faraday’s First Law can be expressed using the following formula:

m = QM/nF

Where:

• m is the mass of the substance deposited or liberated (in grams).
• Q is the total electric charge passed through the electrolyte (in Coulombs).
• M is the molar mass of the substance (in grams per mole).
• n is the number of electrons involved in the reaction.
• F is Faraday’s constant, approximately 96,485 Coulombs per mole.

Faraday’s Second Law

Faraday’s Second Law, also known as the law of equivalent proportions, builds upon the foundation laid by the First Law. This law states that the ratio of the masses of different substances produced or consumed during electrolysis is directly proportional to their equivalent weights. ^[1-4]

Formula

Mathematically, Faraday’s Second Law can be expressed as follows:

m₁/m₂ = E₁/E₂

Where:

• m₁ and m₂ are the masses of different substances produced or consumed during electrolysis.
• E₁ and E₂ are the equivalent weights of the substances.

This equation shows that the ratio of the masses liberated or deposited is equal to the ratio of their equivalent weights. The equivalent weight of an element can be defined as the ratio of its atomic weight and valency.

Equivalent weight = Atomic weight/Valency

Example Illustrating Faraday’s Second Law

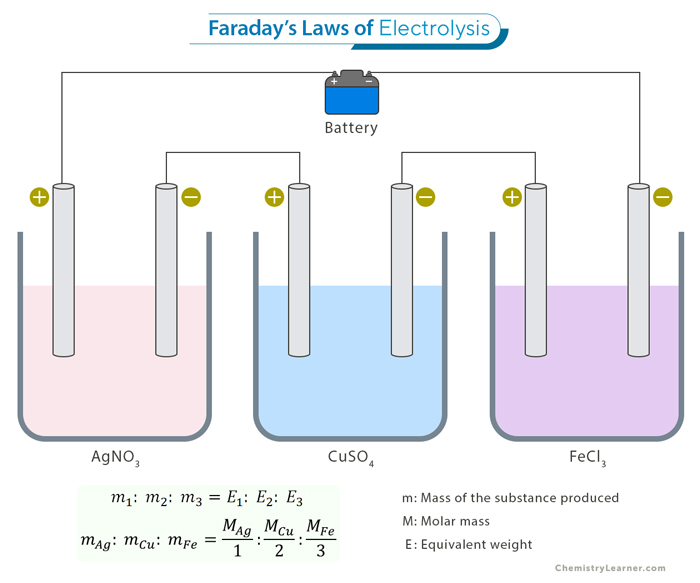
Let us consider the electrolysis of two different electrolytes: copper (II) sulfate (CuSO₄) and silver nitrate (AgNO₃). If we pass the same amount of electric charge through both electrolytes, Faraday’s Second Law tells us that the mass of copper deposited should be proportional to its equivalent weight, as should the mass of silver.

We pass a certain amount of charge through both solutions, depositing 3.17 grams of copper and 10.8 grams of silver.

m_copper/m_silver = 3.17 g/10.8 g

The ratio of their equivalent weights is

E_copper/E_silver = (63.546 g/2)/(107.868 g/1) = 31.773 g/107.868 g = 3.1773 g/10.7868 g

Therefore,

m_copper/m_silver = E_copper/E_silver

The amounts of deposited substances perfectly align with Faraday’s Second Law.

Applications

Faraday’s laws of electrolysis are fundamental in electrochemistry and have numerous practical applications across various industries. ^[1-4]

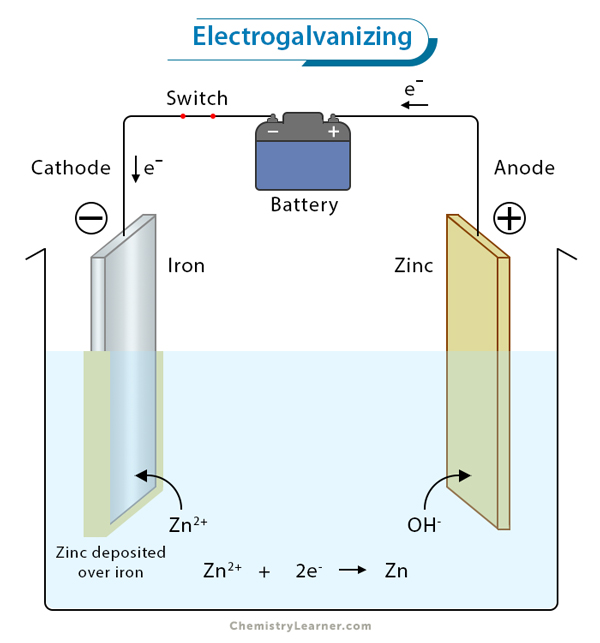
1. Electroplating: Faraday’s laws are extensively utilized in electroplating processes to control the deposition of metals onto surfaces, ensuring uniformity and adherence.

2. Quantitative Analysis: These laws serve as the basis for determining the amount of substance produced or consumed during electrolysis, facilitating precise quantitative analysis in electrochemical experiments.

3. Industrial Processes: Faraday’s laws find application in numerous industrial electrolytic processes, such as metal extraction, purification, and refining, contributing to the efficiency and optimization of production processes.

4. Wastewater Treatment: Electrochemical methods based on Faraday’s laws are employed in wastewater treatment to remove heavy metals and other pollutants, offering environmentally sustainable solutions.