The second law of thermodynamics states that there exists a valuable physical quantity, called entropy, that increases during a natural and spontaneous process. Its change is zero for a reversible process. The second law is also known as the law of increased entropy ^[1-4].

The second law quantifies energy and asserts that a process has a specific direction. The first law does not predict the direction of the process nor guarantee that the process will occur. Thus, the second law was developed to ascertain if a process will happen or not, which is only possible if it satisfies both the first and second laws.

Several eminent scientists have contributed to the second law. These include French physicist Sadi Carnot, German physicist Rudolf Clausius, and Scottish-Irish physicist Lord Kelvin.

Equation

To understand the second law equations, we must first know the mathematical form of entropy. When a system goes from one state to another, its entropy change (ΔS) is defined as the amount of heat (Q) exchanged divided by the temperature (T) at which the exchange takes place ^[1,3-5].

ΔS = Q/T

Therefore, the change in entropy for the system and the surroundings are given as follows:

(ΔS)_sys. = Q_sys./T

 (ΔS)_surr. = Q_surr./T

The total entropy change is the sum of the entropy changes in the system and the surroundings. This total is the entropy change of the universe.

(ΔS)_univ.= (ΔS)_sys. + (ΔS)_surr.= Q_sys./T + Q_surr./T

Reversible Process

For a reversible, isothermal process, the heat lost by the system equals the heat gained by the surroundings. Similarly, the heat gained by the system equals the heat lost by the surroundings. Therefore,

Q_sys. = – Q_surr.

Hence,

(ΔS)_univ. = Q_sys./T – Q_sys./T = 0

Thus, for a reversible, isothermal process, the entropy change of the universe is zero.

Irreversible Process

If the process is irreversible, then the heat absorbed by the system from the surroundings is given by

Q_irrev. = nRT ln (V₂/V₁)

Where

V₁: Initial volume of the system

V₂: Final volume of the system

T: Temperature at which volume change occurs

R: Universal gas constant (R = 8.314 JK^-1M^-1)

n: Number of moles

We assume the system is an ideal gas that expands upon absorbing heat. Then, the entropy change of the universe is

(ΔS)_univ. = Q_irrev./T = (nRT ln (V₂/V₁))/T = nR ln (V₂/V₁)

Which is greater than zero since V₂ > V₁. Therefore,

(ΔS)_univ. > 0

If we combine both processes, we get the entropy change of the universe.

(ΔS)_univ. = (ΔS)_sys. + (ΔS)_surr. ≥ 0

The above inequality implies that (ΔS)_univ. is zero for a reversible process and increases for an irreversible process. The increase in entropy is because there may be work done on the system, resulting in friction and viscosity. Alternatively, there may be a chemical reaction occurring. The second law of thermodynamics leads us to conclude that disorder in the universe is increasing over time.

Example

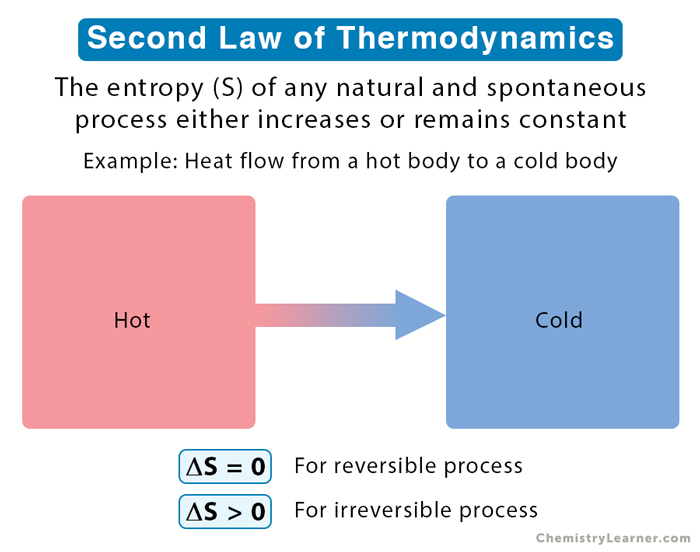
To understand the second law with an example, let us consider a typical irreversible process from real life ^[2,4,5].

Suppose a hot object is put in contact with a cold object. Heat flows from the former to the latter, so the two come to thermal equilibrium. Now, suppose the two are separated. Would they return to their original temperatures? No. Thus, bringing them to the same temperature is irreversible; entropy will increase.

Alternative Statements of the Second Law

The second law of thermodynamics has two alternative statements ^[3,5].

1. Clausius Statement: “It is impossible to construct a device that, operating on a complete cycle, produces no effect other than transferring heat from a cold body to a hot body.”
2. Kelvin-Planck Statement: “It is impossible to construct a device that, operating on a complete cycle, produces no effect other than converting heat directly into work.”

An application of the second law lies in heat engines and refrigerators. The second law places theoretical limits on the performances of these machines. Kelvin-Planck statement implies that no heat engine can have a thermal efficiency of 100%; otherwise, it would violate the second law. For example, a diesel engine has a thermal efficiency of 30%.

In nature, heat flows from a high-temperature region to a low-temperature region, as in the case of a heat engine. The reverse is not possible naturally; otherwise, the second law will be violated. However, a refrigerator can transfer heat from low to high temperatures, aided by work. According to Clausius statement, a refrigerator will not operate unless an external force drives its compressor to perform the desired work.

Any machine that violates the second law of thermodynamics is called the perpetual motion of the second kind.