Order of Reaction
The order of a reaction refers to the relationship between the reactants’ concentrations and the reaction rate. It is the sum of the exponents of the concentrations established from the rate law. The reaction order determines how the concentration affects the reaction rate and which reactant species has the dominating effect [1-4].
Characteristics [1-6]
1. It is the sum of the exponents of the reactants’ concentration in the rate law equation.
2. It is not necessarily equal to the sum of the stoichiometric coefficients of the reactants.
3. It does not depend on the products’ concentrations.
4. Its value can be zero, integer, or fraction.
- A zero-order means that reaction rate does not depend on the reactants’ concentrations.
- A negative order indicates that the reaction rate is inversely proportional to the reactants’ concentrations.
- A positive order means that the reaction rate is directly proportional to the reactants’ concentrations.
- A non-integer order is a complicated relationship between reaction rate and concentration. It is generally observed for complex reactions.
Reaction Order and Rate Law [1-6]
Consider the reaction between the reactants A, B, and C to give products.
aA + bB + cC → Products
Where a, b, and c are the stoichiometric coefficients of A, B, and C. Suppose the experimental rate law is given by
Rate = k [A]x [B]y
Where,
[A]: Concentration of A
x: Reaction order with respect to A
[B]: Concentration of B
y: Reaction order with respect to B
k: Rate constant
From the above rate law equation, the order of reaction is x + y. Note that x and y are not stoichiometric coefficients. The table below lists the values of x + y for the different reaction orders.
| Reaction Name | x + y |
| Zero-order reaction | 0 |
| First-order reaction | 1 |
| Second-order reaction | 2 |
| Third-order reaction | 3 |
Example
Suppose a = 1, b = 2, and c = 3. Then, the reaction is given by
A + 2 B + 3 C → Products
And experimentally, the rate is
Rate = k [A] [B]2
Here, x = 1 and y = 2. The reaction is first-order in A and second-order in B. Therefore, the overall reaction order is 1 + 2 = 3, or a third-order reaction.
While C is present in the reaction, its concentration does not appear in the rate law equation. The reaction is zero-order in C, and the rate does not depend on its concentration. The reason is that C is present in such a vast amount that its concentration change does not affect the reaction rate.
How to Determine the Reaction Order
In the case of an elementary (single-step) reaction, the reaction order is easy to determine. It is the sum of the stoichiometric coefficients of the reactants. However, other methods are applied to determine the order if the reaction occurs in multiple steps. Let us look into these methods [1-6].
Differential Method
The differential method uses experimental data to determine the reaction order. It is also known as the initial rates method. Recall the rate equation.
R = k [A]x [B]y
Which can be written as follows:
ln R = ln k + x ln [A] + y ln [B]
Suppose, in the experiment, the concentration of A changes and that of B remains constant. Then, the above equation reduces to
ln R = x ln [A] + C
Here, x and C are constants. Moreover, R can be determined experimentally. To find x, we use the following steps:
1. Arrange the values of A, ln [A], R, and ln [R] in a table.
2. Plot a graph of ln R vs. ln A.
3. The slope of the graph will give the value of x.
4. Repeat the above process for B to obtain the value of y.
5. After obtaining the values of x and y, the reaction order is x + y.
Integral Method
In this method, the experimental data is used to check which integrated rate law it satisfies. The integrated rate laws are as follows: [4]
Zero-order: [A] = -kt + C
First-order: ln [A] = -kt + [A]o
Second-order: 1/[A] = kt + 1/[A]o
Third-order: 1/[A]2 = 2kt + 1/[A]o2
We measure the concentration of A and keep checking the time t. Then, we proceed with the following steps:
1. Plot a graph of [A] vs. t and check whether it is a straight line.
2. If not, then the reaction is not of zero order.
3. Plot a graph of ln [A] vs. t, and check whether the plot is linear.
4. If not, the order cannot be 1.
5. Plot a graph of 1/[A] vs. t and check if the graph is linear or not.
6. If not, the reaction is not of the second order.
7. Finally, plot a graph of 1/[A]2 vs. t, and check if the plot makes a linear fit.
8. If the graph is linear, the reaction is of the third order.
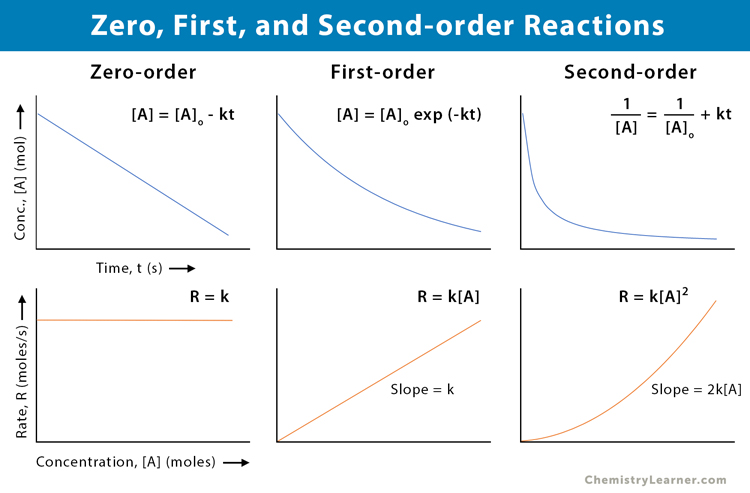
Zero-, First-, and Second-order Reactions
The table below compares and contrasts zero-, first-, and second-order reactions [1-6].
| Property | Zero-order | First-order | Second-order |
|---|---|---|---|
| Rate law | Reaction rate is constant over time and independent of the reactant’s concentrations | Reaction rate is proportional to the first power of the reactant’s concentration | Reaction rate is proportional to the second power of the reactant’s concentration or product of two reactants’ concentrations |
| Rate law equation | -d[A]/dt = k | -d[A]/dt = k [A] | -d[A]/dt = k [A]2 |
| Units of rate constant (k) | mol · L-1 · s-1 | s-1 | mol-1 · L · s-1 |
| Integrated rate law | [A] = -kt + [A]o | ln [A] = -kt + ln [A]o | 1/[A] = kt + 1/[A]o |
| The plot required for the linear fit of experimental data | [A] vs. t | ln [A] vs. t | 1/[A] vs. t |
| The slope of the linear plot | -k | -k | k |
| Half-life | t1/2 = [A]o/2k | t1/2 = 0.693/k | t1/2 = 1/k[A]o |
| Example | Decomposition of nitrous oxide | Decomposition of hydrogen peroxide | Decomposition of nitrogen dioxide |