An adiabatic process is a thermodynamic process in which there is no heat exchange between a system and its surroundings. The system is thermally isolated. The process is carried out so rapidly that heat exchange is impossible within a short period ^{[1– 4]}.

Examples ^[1,2,6]

• In a pneumatic tire, heat is generated rapidly when the gas is compressed.
• Vertical airflow in the atmosphere – Hot air rises and rapidly cools down
• Expansion and contraction of interstellar gas
• Certain parts of the Carnot engine and Diesel engine are adiabatic.
• Gas turbines operating on the Otto cycle and Brayton cycle use adiabatic processes.

Adiabatic Process, First Law of Thermodynamics, and Enthalpy Change

The first law of thermodynamics establishes a relationship between the internal energy (ΔU) of a system, heat transfer (Q), and work done (W). The following equation represents the first law ^[4].

ΔU = Q – W

Since there is no exchange of heat, Q = 0, and the work done is given by

W = – ΔU

It means that if a system does work, energy leaves the system. The work done equals the internal energy change.

The opposite also holds correct. If the surrounding does work on the system, energy enters the latter.

W = ΔU

The first law of thermodynamics in terms of enthalpy change is given by

ΔH = ΔQ + VΔP

For an adiabatic process

ΔH = VΔP

Therefore, the enthalpy change is equal to the flow process work done by the system. This equation applies to open-flow systems like a turbine or pump.

Adiabatic Expansion and Compression

When a gas is expanded adiabatically, its pressure decreases while its volume increases. It results in a decrease in temperature, a process known as adiabatic cooling. When a gas is compressed adiabatically, its pressure increases, and the volume decreases. As a result, the temperature rises, resulting in a phenomenon known as adiabatic heating ^[1,3].

Based on the pressure, volume, and temperature variations, let us study a few equations that govern the adiabatic process.

Adiabatic Process Equations

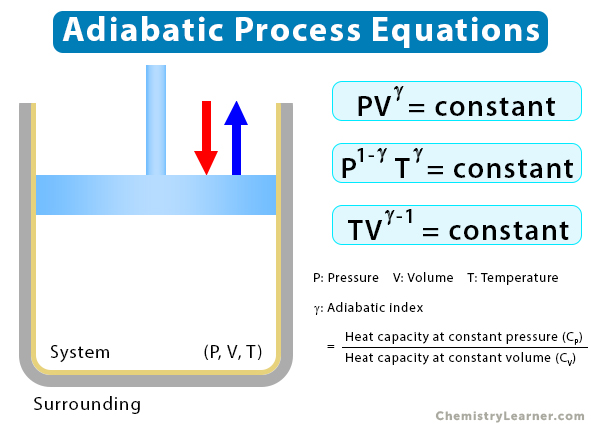
A series of equations establish relationships between pressure (P), volume (V), and temperature (T) for a reversible quasistatic process. In the above section, we mentioned that when pressure decreases, volume increases, and vice versa. Therefore, P and V are inversely proportional, leading to the following equation ^[1-5]:

PV^γ = constant

When the system goes from an initial (i) to a final (f) state, we can rewrite the above equation as follows:

P_iV_i^γ = P_fV_f^γ

Where

P_i: Initial pressure of the gas

V_i: Initial volume of the gas

P_f: Final pressure of the gas

V_f: Final volume of the gas

γ: Adiabatic index

We will use this equation later to calculate the adiabatic work done.

The adiabatic index, γ, is defined as the ratio of the heat capacity at constant pressure (C_P) to the heat capacity at constant volume (C_V).

γ = C_P/C_V

Its value is 1.67 for a monoatomic gas, 1.4 for a diatomic gas, and 1.33 for a non-linear triatomic gas.

Other Relationships

We can combine the PV relationship with the ideal gas law (PV = nRT) to obtain other equations. The relationship between P and T is as follows:

P^1-γT^γ = constant

Furthermore, the relationship between T and V is as follows:

TV^γ-1 = constant

Work Done in Adiabatic Process

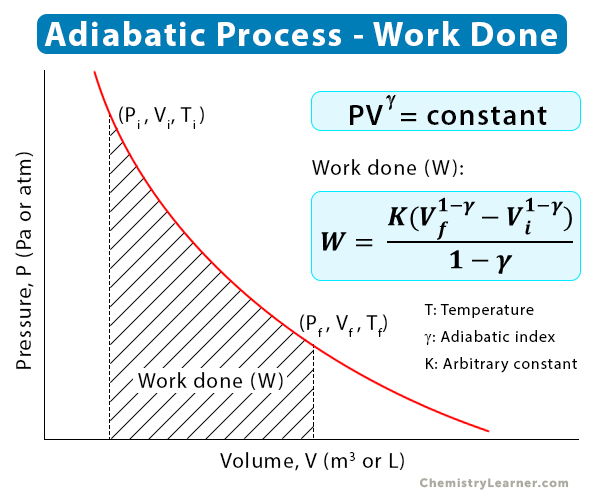
We have already seen how pressure (P) varies with volume (V) when the gas goes from the initial (i) to the final (f) state. This relationship is represented in the P-V curve shown below. We can calculate the work done from this curve. For this purpose, we take an infinitesimal area underneath the P-V curve and integrate it ^[4].

W = -∫PdV

From P-V equation

PV^γ = constant = K

=> P = K/V^γ

Therefore

W = K∫dV/V^γ

=> W = K (V_f^1-γ – V_i^1-γ)/(1 – γ)

Example Problems

Problem 1: Consider pumping air inside the tire of a bicycle using a hand pump. The air inside the pump is a thermodynamic system with well-defined volume, pressure, and temperature. Suppose the nozzle of the tire is blocked. When air is pumped, its volume reduces by ⅓. Calculate the final temperature of the air in the pump if the pump is at room temperature of 27 ^oC initially.

Solution

Since the nozzle is blocked, air cannot flow inside the tire. The sudden decrease in volume can be considered an adiabatic process.

Given T_i = 27 ^oC = 273 + 27 = 300 K           V_f/V_i = ⅓              g = 1.4 (since air is diatomic)

We use the following equation:

T_iV_i^γ-1 = T_fV_f^γ-1

=> T_f = T_i (V_i/V_f)^γ-1

=> T_f = 300 K (3)^1.4-1

=> T_f = 466 K