The Arrhenius equation is one of the most important equations in physical chemistry. It describes the relationship between the reaction rate and the temperature for many chemical reactions. It is a simple and accurate formula used to study the temperature dependence of the rate constant ^[1-4].

Swedish scientist Svante Arrhenius proposed the equation in 1889 by combining the concept of activation energy and the Boltzmann distribution law.

Form of Arrhenius Equation

The Arrhenius equation is rooted in experimental observations and cannot be derived logically. The common form of the Arrhenius equation is given by an exponential formula, as shown below ^[1-5].

k = A exp(-E_A/RT)

Where

k : rate constant

A : pre-exponential factor

E_A : activation energy

T : temperature

R : universal gas constant ( = 8.314 J/mol-K)

The Arrhenius equation has a massive and significant application in determining chemical reaction rates and calculating the activation energy. The equation tells us that the rate constant is decaying, not with time but with the term E_A/RT. The term RT represents the average kinetic energy of the molecules. So, the rate constant decays with the ratio of the activation energy over average kinetic energy. The larger the ratio, the smaller the rate constant. High temperature and low activation energy result in a large rate constant and thus accelerate the chemical reaction.

Units

The unit of the various variables and constants of Arrhenius equations are as follows:

Activation energy: J/mol

Temperature: K or Kelvin

Universal gas constant (R): J/mol·K

Pre-exponential factor and rate constant: s^-1 for a first-order reaction

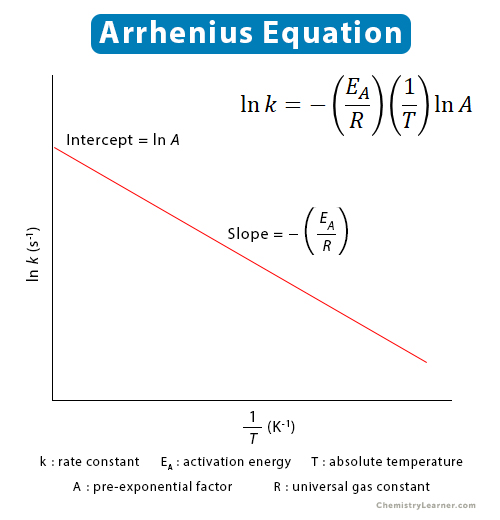
Arrhenius Plot

Another way to write the Arrhenius equation is by taking the logarithm of both sides ^[1-5].

ln (k) = ln (A) – E_A/RT

Rearranging the equation gives

ln (k) = (– E_A/R) (1/T) + ln (A)

The above equation is more convenient and easier to interpret graphically than the exponential equation. It is in the form of a straight line given by y = mx + c. Let us look at the various terms in this equation.

Dependent variable: y = ln (k)

Independent variable: x = (1/T)

Slope: m = (-E_A/R)

Intercept: c = ln (A)

A plot of ln (k) vs. 1/T gives a straight line with slope given by-E_A/R and intercept given by ln (A). This plot is known as the Arrhenius plot and is shown in the image below.

Arrhenius plot is conveniently used to determine the activation energy and the pre-exponential factor. Multiplying the slope by the negative of the universal gas constant gives activation energy.

E_A = m x (-R)

Taking the exponential of the intercept gives the pre-exponential factor.

A = exp (c)

Arrhenius Equation and Activation Energy

The exponential term E_A/RT in the Arrhenius equation implies that the rate constant, hence the reaction rate, of a chemical reaction increases exponentially as the activation energy decreases. A chemical reaction with low activation energy does not require much energy to reach the transition state. It proceeds faster than a reaction with large activation energy. As the activation energy of a catalyzed reaction is lower than that of an uncatalyzed reaction, the former occurs faster than the latter. The reaction rate is impacted more by temperature changes than the activation energy for the uncatalyzed reaction ^[1].

Arrhenius Equation and Frequency Factor

The pre-exponential factor A is also known as the frequency factor since it includes the frequency of molecular collisions and their orientations. It is not directly involved in the determination of the activation energy. However, when multiplied by the exponential term, it contributes to the rate constant and thus the reaction rate ^[1].

Combining the Arrhenius equation with Maxwell-Boltzmann law, we find that the term exp (-E_A/RT) represents the fraction of reactant molecules that possess enough kinetic energy to react. Depending on E_A and T, this fraction can be anywhere between 0 and 1.

Suppose E_A = 0. Then,

k = A

It means that A is the fraction of molecules that would react if the activation energy were zero.

Two-point Form of Arrhenius Equation

The Arrhenius equation can determine an unknown rate constant or temperature without using the pre-exponential factor. For this purpose, the rate constant is measured for two different temperatures T₁ and T₂. The two-point form of the Arrhenius equation is written as follows ^[1,2]:

ln (k₁) = (– E_A/R) (1/T₁) + ln (A)

ln (k₂) = (– E_A/R) (1/T₂) + ln (A)

Rewriting the 2^nd equation

ln (A) = ln (k₂) – (E/_AR) (1/T₂)

Substituting ln (A) in the 1^st equation

ln (k₁) = – (E_A/R) (1/T₁) (1/T₁) + ln (k₂) – (E_A/R) (1/T₂)

Or, ln (k₁) – ln (k₂) = – (E_A/R) (1/T₁ – 1/T₂)

Or, ln (k₁/k₂) = – (E_A/R) (1/T₁ – 1/T₂)

Hence, one can determine the unknown variable by knowing any three variables, k₁, k₂, T₁, and T₂.

Example Problems and Solutions

Problem 1: The rate constant of a reaction at 25.0 °C was measured to be 7.4 × 10^-2 s^-1. If the frequency factor is 1.8 × 10¹⁴ s^-1, what is the activation energy? (R = 8.314 JK^-1M^-1)

Solution:

Given

k = 7.4 × 10^-2 s^-1

A = 1.8 × 10¹⁴ s^-1

T = 25.0 °C = 25 + 273 = 298 K

From Arrhenius equation

ln (k) = (– E_A/R) (1/T) + ln (A)

Or, (E_A/R) (1/T) = ln (A) – ln (k)

Or, E_A = RT (ln (A) – ln (k))

Or, E_A = 8.314 JK^-1M^-1 x 298 K x (ln (1.8 × 10¹⁴ s^-1) – ln (7.4 × 10^-2 s^-1))

Or, E_A = 74873 JM^-1 or 74.9 kJM^-1

Problem 2: The activation energy for a reaction is 33.7 kJ/mol. The rate constant for the reaction is 4.5 x 10^-3 s^-1 at 47 °C. Calculate the rate constant at 125 °C. (R = 8.314 JK^-1M^-1)

Solution:

Given

E_A = 33.7 kJ/mol

k₁ = 4.5 x 10^-3 s^-1

T₁ = 47 °C = 273 + 47 = 320 K

T₂ = 125 °C = 273 + 125 = 398 K

From Arrhenius equation,

ln (k₁/k₂) = – (E_A/R) (1/T₁ – 1/T₂)

Or, ln (4.5 x 10^-3 s^-1/k₂) = – (33.7 x 10³ J M^-1 / 8.314 JK^-1M^-1) (1/320 – 1/398)

Or, ln (4.5 x 10^-3 s^-1/k₂) = 2.48 JM^-1

Or, 4.5 x 10^-3 s^-1/k₂ = 11.9

Or, k₂ = 4.5 x 10^-3 s^-1/11.9

Or, k₂ = 3.78 x 10^-4 s^-1