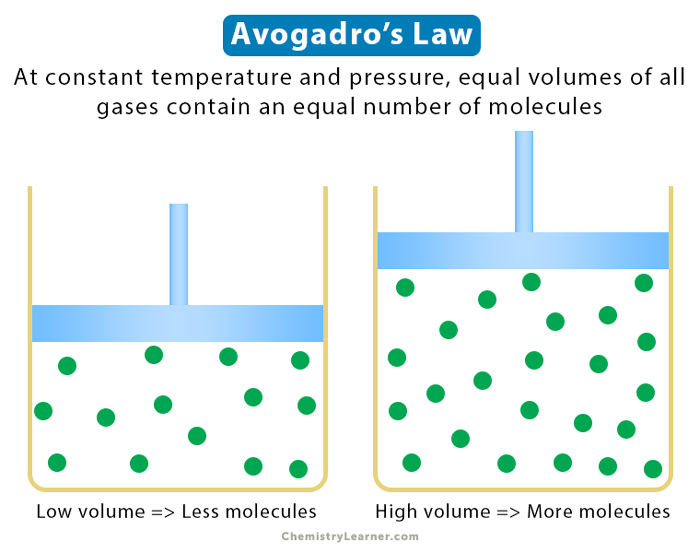
Avogadro’s law states that equal volumes of different gases contain an equal number of molecules under the same pressure and temperature conditions. This law is valid for ideal gases at low pressures and high temperatures ^[1-4].

Italian physicist Amedeo Avogadro was the first to state the hypothetical law in 1811.

Avogadro’s Law Formula

According to Avogadro’s hypothesis, the volume (V) of a gas is directly proportional to the number of moles (n) ^[1-4].

V ∝ n

Where

V : Volume

n : Number of moles

The above proportionality can be written as follows:

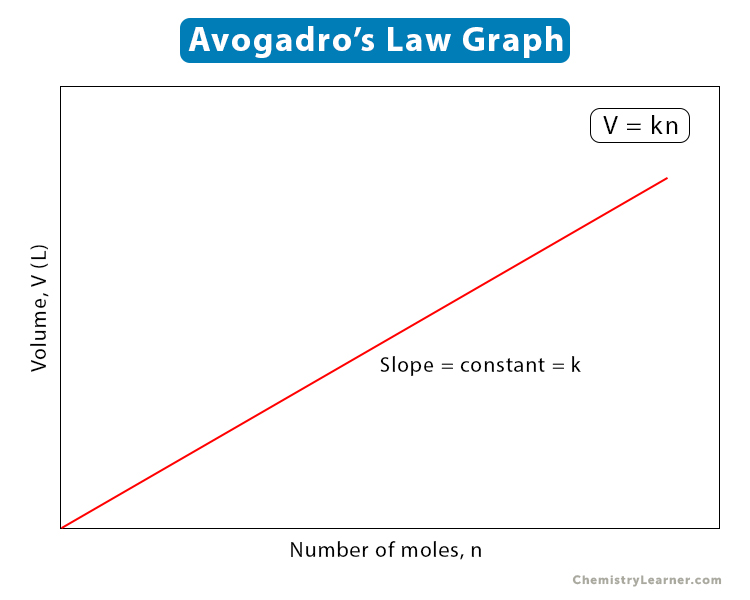
V = kn

Where

k : proportionality constant

This equation can be represented as a graph.

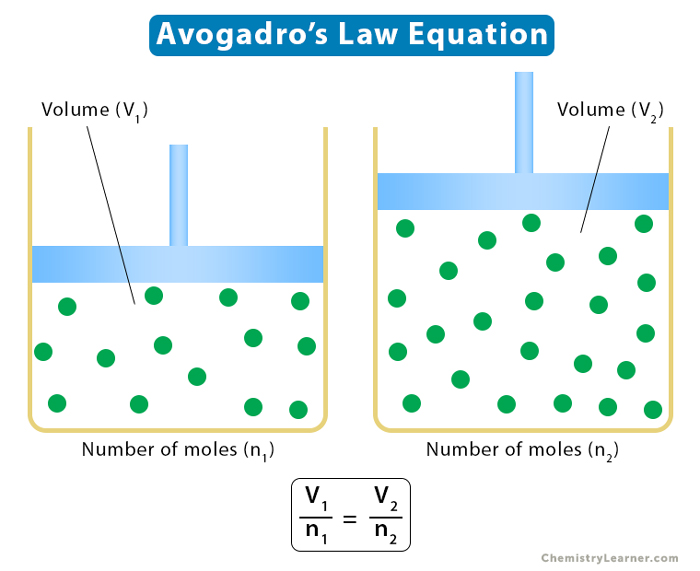
Consider a gas with n₁ moles with a volume V₁. Suppose the number of moles increases to n₂ such that the volume increases to V₂, then

V₁ = kn₁ and V₂ = kn₂

Dividing one equation by the other and rearranging,

V₁/n₁ = V₂/n₂

The above equation can be used to compare two gases at the same temperature and pressure conditions. Also, the number of molecules in a given volume of an ideal gas is independent of their size or the molar mass.

Derivation

In order to derive Avogadro’s gas law, let us look at the ideal gas equation.

PV = nRT

Or, V/n = RT/P

Where

P : Pressure

V : Volume

n : Number of moles

R : Universal gas constant

T : Temperature

At constant pressure and temperature, the right-hand side is constant. Let, k = RT/P. Then,

V/n = k

Thus, the volume is proportional to the number of moles of the gas.

Avogadro’s Number

Let us rewrite the ideal gas law as follows:

PV = (N/N_A)RT

The ratio N/N_A gives the number of moles or n = N/N_A. Here, N is the number of molecules in the gas, and N_A is known as Avogadro’s number. It is the number of molecules present in one mole of a substance. Its value is 6.023 x 10²³.

Molar Volume

Avogadro’s number can be used to calculate the molar volume. For one mole of a gas, n = 1 and V = k. Therefore, one has to know the value of k at standard temperature and pressure (STP). At STP, the pressure (P) is 101.325 kPa, and the temperature (T) is 273.15 K. The universal gas constant R has a value of 8.314 L·kPa·M^-1·K^-1. Putting in all the values, we get

k = RT/P

Or, k = 8.314 L·kPa·M^-1·K^-1 x 273.15 K /101.325 kPa

Or, k = 22.4 LM^-1

Examples

Below are some examples of Avogadro’s law in everyday life ^[5].

• Respiration: When we respire, we breathe in oxygen. The more we breathe, the more our lungs will expand.
• Deflation: When the air is released from an inflated tire, the number of moles decreases. The shape of the tire also changes since its volume decreases.
• Inflation: When a water tube is inflated by pumping air inside, the number of air molecules increases. Thus, the tube is inflated, and its volume increases.

Applications and Uses ^[1]

• Explains Gay-Lussac’s law
• Determines the atomicity of the gases
• Determines the molecular formula of a gaseous compound
• Gives the relationship between gram molecular mass and gram molecular volume of gas
• Determines the relationship between molecular mass and vapor density of a gas

Problems and Solutions

Problem 1: Two moles of helium gas fill up an empty balloon to a volume of 2.5 L. What would be the volume of the balloon if an additional 1.5 moles of helium gas is added at constant temperature and pressure.

Solution:

Given

n₁ = 2 mol

V₁ = 2.5 L

n₂ = 2 mol + 1.5 mol = 3.5 mol

From Avogadro’s law,

V₁/n₁ = V₂/n₂

Therefore, the final volume of the balloon is

 V₂ = V₁·n₂ /n₁ = (2.5 L x 3.5 mol)/2 mol = 4.375 L

Problem 2: 40 g of nitrogen gas is kept in a 2.5 L container. The gas exerts a pressure of 2 atm on the container. If pressure is kept constant, what is the final amount of gas in grams present in the container if gas is added until the volume has increased to 4.0 L?

Solution:

Given

Mass of nitrogen = 40 g => n₁ = Mass/Molar mass = 40 g/28 gM^-1 = 1.43 M

V₁ = 2.5 L

V₂ = 4 L

From Avogadro’s law,

V₁/n₁ = V₂/n₂

Or, n₂ = n₁ x V₂/V₁

Or, n₂ = 1.43 M x 4 L/2.5 L

Or, n₂ = 2.29 M

Therefore, amount of nitrogen

= 2.29 M x 28 gM^-1 = 64 g