Bohr Model

What is Bohr Model

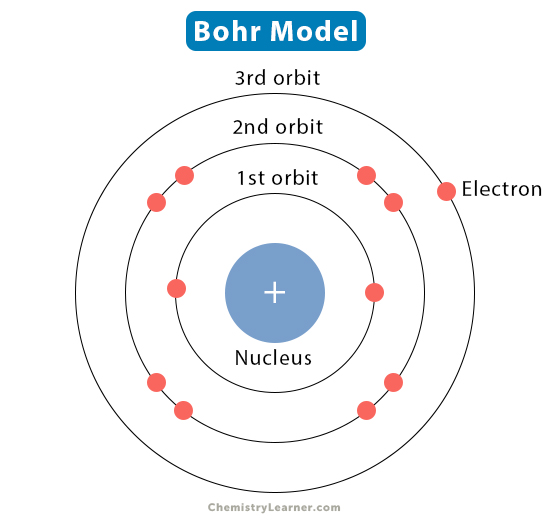
The Bohr model represents the structure of an atom developed by Danish physicist Niels Bohr in 1913. According to this model, the atomic structure is similar to that of the solar system. The nucleus represents the sun, and the electrons represent the planets orbiting around the nucleus. Unlike gravitational forces that keep planets in their orbits, electrons are held in their orbits by electrostatic forces. Thus, the Bohr model is often called the planetary model ^[1-4].

Salient Features of the Bohr Model ^[2]

• Electrons move around the nucleus in orbits of well-defined radius.
• Electrons orbiting in orbits do not interact with each other.
• The energy of the electron depends on the principal quantum number n.
• According to Planck’s relation, when an electron moves from one orbit to another, it absorbs or emits radiation.

Development of the Bohr Model ^[1-3]

How is Bohr’s Atomic Model Different from Rutherford’s Model

Several experiments done by New Zealand physicist Ernest Rutherford established that an atom consists of a positively charged nucleus surrounded by a cloud of negatively charged electrons. Rutherford developed his model in 1911, which is also known as the classical model. However, this model has a few drawbacks. It fails to explain why the electrons do not spiral inwards during their motion and collapse into the nucleus. In other words, it does not explain why atoms are stable. Moreover, the classical model considers that electrons revolving around orbits emit continuous radiation, which fails to explain the atomic line spectra of many atoms.

Bohr applied his ideas to the Rutherford model, and hence, his model is also called the Bohr-Rutherford model. He used quantum mechanics to explain the spectral lines emitted by the hydrogen atom. According to Bohr, electrons orbit around the nucleus in discrete circular orbits with well-defined radii, which depend on the principal quantum number n. While observing the emission spectra of the hydrogen atom, Bohr was able to account for the fine spectral lines. He proposed that when an electron jumps from a higher orbit to a lower orbit or one closer to the nucleus, it emits radiation in the form of light.

Bohr Model Applied to Hydrogen Atom

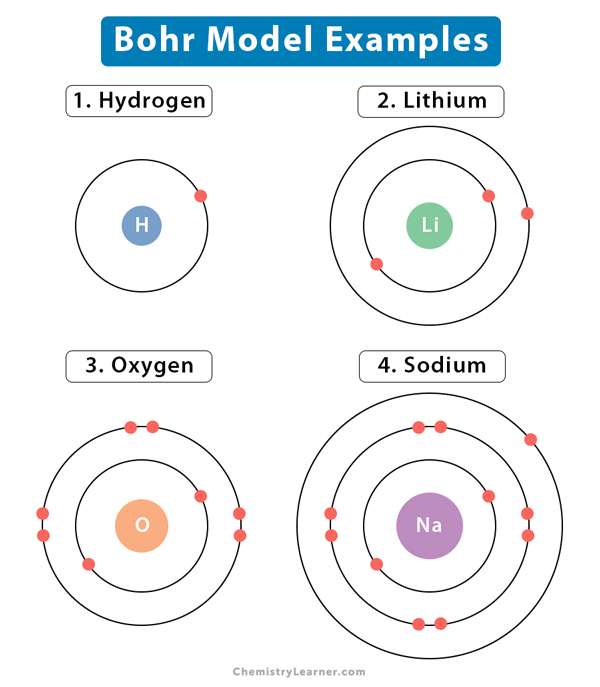
The simplest example of the Bohr model is the hydrogen or hydrogen-like atom consisting of one electron orbiting around the nucleus. In its ground state, the electron in the first orbit is represented by n = 1. When incoming radiation falls on the atom, the electron absorbs it and jumps to a higher state (n > 1), known as the excited state. However, this excited state is only temporary. The electron relaxes to a lower state, simultaneously releasing electromagnetic radiation in the form of light. It has been experimentally observed that only specific transitions are allowed. For example, the transition from n ≥ 3 to n = 2 level results in a transmission line called the Balmer series. An advantage of the Bohr model is that it could explain the absorption and emission spectra of hydrogen and hydrogen-like atoms.

Bohr Model Equation

Bohr resolved the fallacy of the classical model by incorporating Planck’s quantum theory and Einstein’s photoelectric effect. According to Bohr, the orbits in which the electrons reside are quantized. The radius, angular momentum, and energy take specific values only ^[1,2].

1. Radius

The radius of the n-th orbit is given by,

r_n = n² x r_B

Where,

r_n : radius of the n-th orbit

r_B : smallest electron radius of the hydrogen atom, known as Bohr radius ( = 0.529 x 10^-10 m)

n : principal quantum number (n = 1,2,3…)

Only shells of radii given by the above equation are allowed.

2. Energy

By the early 20^th century, physicists Max Planck and Albert Einstein developed the quantum theory, which states that matter absorbs and emits radiation in discrete packets known as quanta. According to this theory, electromagnetic radiation can exist as both a wave and a particle. When it exists as a particle, it is called a photon. The energy carried by a photon is given by,

E = hν

Where,

h : Planck’s constant ( = 6.626 x 10^-34 J.s)

ν : frequency of radiation

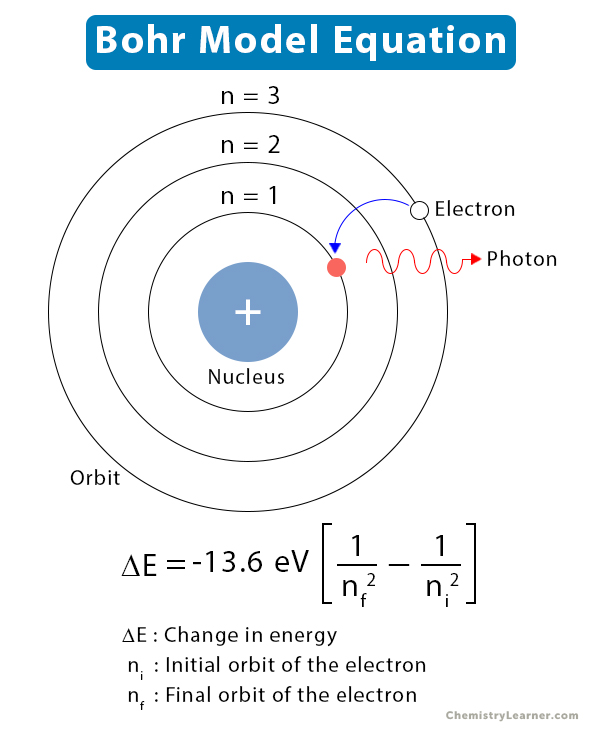
Bohr was able to apply this quantization idea to his atomic orbital theory and found that the orbital energy of the electron in the n^th orbit of a hydrogen atom is given by,

E_n = -13.6/n² eV

According to the Bohr model, electrons can only absorb energy from a photon and move to an excited state if the photon has an energy equal to the energy difference between the two energy levels. The excited state is unstable, and the electron jumps to a lower level while releasing a photon. The energy released by an electron when it jumps from a higher orbit to a lower orbit is,

ΔE= E_f – E_i

Where,

E_i : initial energy of the electron

E_f : final energy of the electron

ΔE : change in electron energy

Or, ΔE= -13.6 eV (1/n_f² – 1/n_i²)

Apply Planck’s relation for quantized energy,

ΔE= hν

This energy is negative and so taking the magnitude,

|ΔE| = hν

Or, 13.6 eV (1/n_f² – 1/n_i²) = hc/λ

Or, 1/λ = (13.6 eV/hc )(1/n_f² – 1/n_i²)

Or, 1/λ = R_H (1/n_f² – 1/n_i²)

Where,

c : speed of light ( = 3 x 10⁸ m/s)

λ : wavelength of radiation ( = c/ν)

R_H : Rydberg constant ( = 13.6 eV/hc = 1.097 x 10⁷ m^-1)

Therefore, the wavelength and the frequency of the emitted photon depend upon the principal quantum numbers of the two atomic levels.

3. Angular Momentum

Bohr postulated that the angular momentum is also quantized, and its formula is given by,

L = nh/2π

An advantage of the Bohr model is that the experimental values of radii and energies agree with the calculated values.

Limitations of the Bohr Model ^[7]

• It considers the electron orbits to be circular, similar to the earlier classical models
• It violates Heisenberg Uncertainty Principle by assuming that the electron’s orbital radius and angular momentum can be calculated concurrently
• It does not apply to multi-electron atoms and cannot explain their spectra
• It does not explain why some spectral lines are more intense than others
• It does not explain the splitting of the spectral lines in the presence of a magnetic field. These lines are known as doublets, and the phenomenon is called Zeeman Effect.

Practice Problems

Problem 1. A photon is emitted as an atom makes a transition from n = 5 to n = 2 level. What is the frequency, wavelength, and energy of the emitted photon? (Planck’s constant, h = 4.135 x 10^-15 eV.s) (Speed of light, c = 3 x 10⁸ m/s)

Solution: Given,

n_f = 5

n_i = 2

Therefore, the energy is

E = 13.6 eV (1/n_f² – 1/n_i²)

Or, E = 13.6 eV (1/5² – 1/2²)

Or, E = – 2.856 eV

The energy is negative because the photon is emitted.

The frequency can be calculated as follows.

|E| = hν

Or, ν = |E|/h = 2.856 eV/4.135 x 10^-15 eV.s

Or, ν = 7 x 10¹⁴ Hz

And, the wavelength is,

λ = c/ν = 3 x 10⁸ m/s x 7 x 10¹⁴ Hz

Or, λ = 4.29 x 10^-7 m or 429 nm

Problem 2. What is the energy in electron volts of the photon produced when an electron in a hydrogen atom moves from an orbit with n = 4 to another orbit with n = 2?

Solution: Given,

n_f = 4

n_i = 2

Therefore, the energy is

E = 13.6 eV (1/n_f² – 1/n_i²)

= 13.6 eV (1/4² – 1/2²)

= – 2.25 eV

The negative sign indicates that the electron releases energy.