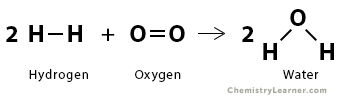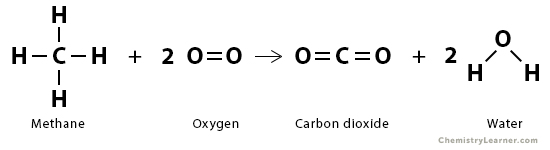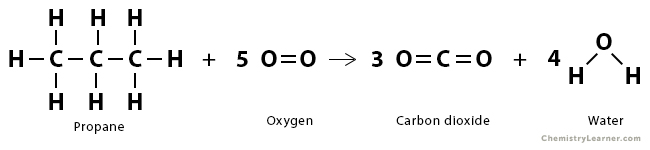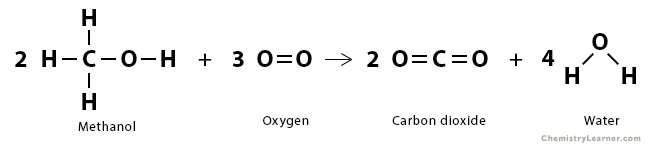Bond Enthalpy
Table of Contents
Bond enthalpy measures the energy stored in a bond between two atoms. It is the energy required to symmetrically cleave a bond when a compound is in its gaseous phase. By symmetrical cleaving, we mean that the bond breaks so that each atom gains one electron and forms a radical [1-4].
Energy must be added to break a chemical bond. Therefore, bond enthalpy values are positive and are measured in the unit of kJ/mol. Higher values of bond enthalpy indicate strong bonds. It means that much energy is required to break the bond. The average values of bond enthalpy can be found in reference tables. These are only approximate values. The actual values depend on the neighboring atoms of the molecule under consideration.
Bond Enthalpy Table
The following chart gives the average bond enthalpy values of a few bonds [4].
| Bond | Bond Enthalpy (kJ/mol) | Bond | Bond Enthalpy (kJ/mol) |
|---|---|---|---|
| C – H | 413 | S – Cl | 253 |
| C – C | 348 | S – Br | 218 |
| C – N | 293 | S – S | 266 |
| C – O | 358 | F – F | 155 |
| C – F | 485 | Cl– F | 253 |
| C – Cl | 328 | Cl – Cl | 242 |
| C – Br | 276 | Br – F | 237 |
| C – I | 240 | Br – Cl | 218 |
| C – S | 259 | Br – Br | 193 |
| N – H | 391 | I – Cl | 208 |
| N – N | 163 | I – Br | 175 |
| N – O | 201 | I – I | 151 |
| N – F | 272 | Si – H | 323 |
| N – Cl | 200 | Si – Si | 226 |
| N – Br | 243 | Si – C | 301 |
| H – H | 436 | Si – O | 368 |
| H – F | 567 | C=C | 614 |
| H – Cl | 431 | C≡C | 839 |
| H – Br | 366 | C=N | 615 |
| H – I | 299 | C≡N | 891 |
| O – H | 463 | C=O | 799 |
| O – O | 146 | C≡O | 1072 |
| O – F | 190 | N=N | 418 |
| O – Cl | 203 | N≡N | 941 |
| O – I | 234 | O=O | 495 |
| S – H | 338 | S=O | 523 |
| S – F | 327 | S=S | 418 |
Examples
1. Hydrogen Chloride (HCl)
The energy required to dissociate one mole of gaseous HCl into gaseous H and Cl radicals is +431 kJ/mol.
2. Methane (CH4)
The energy required to cleave one C-H bond is +413 kJ/mol. In CH4, there are four C-H bonds. Therefore, the average energy required to dissociate one mole of CH4 into gaseous H and C radicals is 4 x 414 kJ/mol = +1656 kJ/mol.
How to Calculate Enthalpy of Reaction from Bond Enthalpy
To calculate the enthalpy of reaction from bond enthalpy, we apply the following steps [1-4]:
Step 1: Find out which bonds will break and their bond enthalpies.
Step 2: Add up the bond enthalpies of the broken bonds.
Step 3: Find the new bonds that will form in the products. Then, find their bond enthalpies and switch the sign from positive to negative. The reason is that energy is released when new bonds are formed, and the energy released is always negative.
Step 4: Add the bond enthalpies of the new bonds.
Step 5: Add the total values for breaking and forming bonds to get the enthalpy of reaction.
The following formula gives the heat of reaction (ΔHrxn) from bond enthalpy.
ΔHrxn = ΣΔHbonds broken + ΣΔHbonds formed
Examples
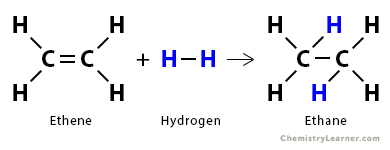
1. Consider the hydrogenation of ethene (C2H4) to give ethane (C2H6).
C2H4 (g) + H2 (g) → C6H6 (g)
We need to break the C=C bond in C2H6 and H-H bond. We need to form three new bonds in C2H6: two C – H bonds and one C – C bond. From the bond enthalpy table above, we have the following information.
| Bond | Bond Enthalpy (kJ/mol) | Broken or Formed |
|---|---|---|
| C = C | 614 | Broken |
| H – H | 436 | Broken |
| C – H | 413 | Formed |
| C – C | 348 | Formed |
The energy required to break the desired bonds is
ΣΔHbonds broken = 614 kJ/mol + 436 kJ/mol = 1050 kJ/mol
The energy liberated when new bonds form is
ΣΔHbonds formed = – 2 x 413 kJ/mol – 384 kJ/mol = – 1210 kJ/mol
Therefore, the enthalpy of reaction is
ΔHrxn = 1050 kJ/mol – 1210 kJ/mol = -160 kJ/mol
2. Consider the formation of water (H2O) from hydrogen (H2) and oxygen (O2).
2 H2 (g) + O2 (g) → 2 H2O (g)
We need to break two H-H bonds and one O=O bond. We need to form four OH bonds. From the bond enthalpy table above, we have the following values.
| Bond | Bond Enthalpy (kJ/mol) | Broken or Formed |
|---|---|---|
| H – H | 436 | Broken |
| O = O | 495 | Broken |
| O – H | 463 | Formed |
The energy required to break the desired bonds is
ΣΔHbonds broken = 2 x 436 kJ/mol + 495 kJ/mol = 1367 kJ/mol
The energy liberated when new bonds form is
ΣΔHbonds formed = – 4 x 463 kJ/mol = – 1852 kJ/mol
Therefore, the enthalpy of reaction is
ΔHrxn = 1367 kJ/mol – 1852 kJ/mol = -485 kJ/mol
When a Liquid is Present
So far, we have assumed that all substances involved in the chemical reaction are in their gaseous state. However, suppose one of the substances is in a liquid state. In that case, the heat of reaction cannot be directly calculated from the bond enthalpies. A new term, heat of vaporization (ΔHvap), must be introduced. The heat of vaporization is the enthalpy change when one mole of a substance is vaporized at its boiling point at standard pressure.
Example
Consider the combustion of methane (CH4) in the presence of oxygen (O2) to form carbon dioxide (CO2) and water (H2O) at standard temperature and pressure.
CH4 (g) + 2 O2 (g) → CO2 (g) + 2 H2O (l)
We need to break four C – H bonds and two O = O bonds. We must form two C = O bonds and four O – H bonds. Aside, we need to convert liquid water into water vapor. From the bond enthalpy table above, we have the following:
| Bond | Bond Enthalpy (kJ/mol) | Broken or Formed |
|---|---|---|
| C – H | 413 | Broken |
| O = O | 495 | Broken |
| C = O | 799 | Formed |
| O – H | 463 | Formed |
The energy required to break the desired bonds is
ΣΔHbonds broken = 4 x 413 kJ/mol + 2 x 495 kJ/mol = 2642 kJ/mol
The energy liberated when new bonds form is
ΣΔHbonds formed = – 2 x 799 kJ/mol – 4 x 463 kJ/mol = – 3450 kJ/mol
The energy liberated when two moles of water vapor are transformed into liquid water is = – 2 x 41 kJ/mol = -82 kJ/mol
Therefore, the enthalpy of reaction is
ΔHrxn = 2642 kJ/mol – 3450 kJ/mol – 82 kJ/mol = -890 kJ/mol
Solved Problems
Problem 1: The complete combustion of propane can be represented by the following equation:
CH3CH2CH3 (g) + 5 O2 (g) → 3 CO2 (g) + 4 H2O (g)
Find the enthalpy of reaction.
We use the following equation to calculate the heat of reaction (ΔHrxn).
ΔHrxn = ΣΔHbonds broken + ΣΔHbonds formed
The following bonds are broken:
| Bond | Bond Enthalpy (kJ/mol) | Number of bonds broken |
|---|---|---|
| C – H | 413 | 8 |
| O = O | 495 | 5 |
| C – C | 348 | 2 |
The total amount of energy required to break the desired bond is
ΣΔHbonds broken = 8 x 413 + 5 x 495 + 2 x 348 = 6475 kJ/mol
The following bonds are formed:
| Bond | Bond Enthalpy (kJ/mol) | Number of bonds form |
|---|---|---|
| C = O | 799 | 6 |
| O – H | 463 | 8 |
The total amount of energy released when new bonds form is
ΣΔHbonds formed = -6 x 799 – 8 x 463 = -8498 kJ/mol
Therefore, the enthalpy of reaction is
ΔHrxn = ΣΔHbonds broken + ΣΔHbonds formed
=> ΔHrxn = 6475 kJ/mol – 8498 kJ/mol
=> ΔHrxn = -2023 kJ/mol
Problem 2: Consider the oxidation reaction of methanol (CH3OH) to produce carbon dioxide (CO2) and water (H2O).
2 CH3OH (g) + 3 O2 (g) → 2 CO2 (g) + 4 H2O (g)
Find the enthalpy of reaction.
Solution
We use the following equation to calculate the heat of reaction (ΔHrxn).
ΔHrxn = ΣΔHbonds broken + ΣΔHbonds formed
The following bonds are broken:
| Bond | Bond Enthalpy (kJ/mol) | Number of bonds broken |
|---|---|---|
| C – H | 413 | 6 |
| O – H | 463 | 2 |
| C – O | 358 | 2 |
| O = O | 495 | 3 |
The energy required to break the bonds is:
ΣΔHbonds broken = 6 x 413 + 2 x 463 + 2 x 358 + 3 x 495 = 5605 kJ/mol
The following bonds are formed:
| Bond | Bond Enthalpy (kJ/mol) | Number of bonds broken |
|---|---|---|
| C = O | 799 | 4 |
| O – H | 463 | 8 |
The total amount of energy released when new bonds form is
ΣΔHbonds formed = -4 x 799 – 8 x 463 = -6900 kJ/mol
Therefore, the enthalpy of reaction is
ΔHrxn = ΣΔHbonds broken + ΣΔHbonds formed
=> ΔHrxn = 5605 kJ/mol – 6900 kJ/mol
=> ΔHrxn = -1295 kJ/mol