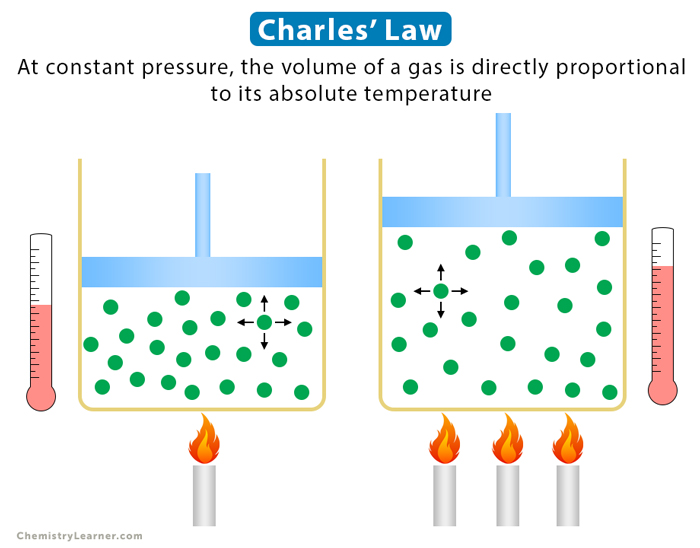
Charles’ law is an experimental gas law that describes how gases expand when heated. It gives a formal relationship between temperature and volume. Charles’ law states that the volume occupied by a gas at constant pressure is proportional to its temperature. In other words, if gas is heated by keeping pressure and mass constant, it will expand ^[1-4].

French physicist J.A.C. Charles first suggested an empirical relationship between temperature and pressure in 1787.

Explanation

Increasing the temperature of a gas confined to a particular volume causes individual gas molecules to move faster. As they move faster, the molecules encounter the walls of the container more often and with greater force. As a result, the pressure is increased. However, if the container volume increases, the number of strikes with the walls decreases. The pressure returns to its initial value ^[1-4].

Equation ^[1-4]

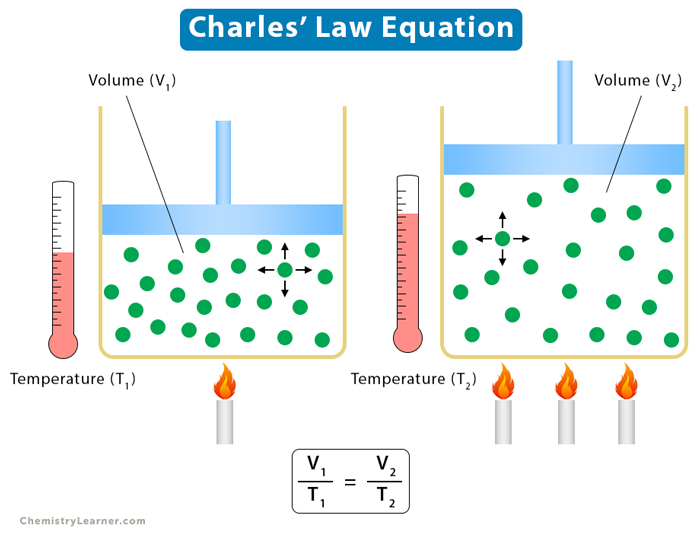
Suppose V is the volume of the gas and T is its temperature. According to Charles’ law,

V ∝ T

Or, V = kT

Where

V : Volume of the gas in liters or m³

T : Temperature of the gas in absolute scale or Kelvin

k : Proportionality constant

The above equation is shown in the graph below.

From the above equation, it is evident that as the temperature increases, the volume also increases. Similarly, if the temperature decreases, the volume decreases.

Charles’ law can be used to compare two states or conditions of a gas. Suppose a gas at temperature T₁ has volume V₁. It expands or contracts such that its final volume and temperature are V₁ and T₁, respectively. Then,

V₁ = kT₁ and V₂ = kT₂

Dividing one by the other

V₁/T₁ = V₂/T₂

The above equation gives the relationship between the initial and final conditions of the gas.

Examples

Here are some examples of Charles’ law in everyday life ^[5,6].

• A hot air balloon rises because burning propane heats the air. The air expands, thereby increasing the volume and decreasing the density. The envelope of air inside the balloon is lighter than the air outside, making it easier for the balloon to rise.
• We breathe air and expand the lungs. In winter, due to cold air inside them, the lungs shrink. Hence, running and jogging become challenging to do in winter.
• A pool tube can inflate or shrink. On a cold winter day, the water temperature is near freezing. Hence, the air temperature inside the tube is low, and the tube shrinks. The opposite happens on a hot summer day. The air inside the tube is heated, and its temperature rises. As a result, the tube inflates.
• The dent in a ping pong ball can be repaired by immersing it in warm water. The high temperature of water raises the air temperature inside the ball. The air expands, and its pressure forces repair the dent.
• The volume of air inside a tire is affected by the outside temperature. On a cold day, the low temperature outside reduces the air temperature inside. Hence, the tire is deflated. On a hot day, the reverse happens. The high temperature outside increases the air temperature inside. As a result, the tire inflates.
• A helium balloon behaves similarly to a tire. It crumbles when the balloon is taken out of a house on a cold day. When brought back inside a warm room, the balloon gets back to its original shape.

Problems and Solutions

Problem 1: What change in volume results if 4 L of oxygen is cooled by 6.0 °C from 120 °C?

Solution:

Given

V₁ = 4 L

T₁ = 120 + 273 = 393 K

T₂ = 114 + 273 = 387 K

From Charles’ law,

V₁/T₁ = V₂/T₂

Or, V₂ = V₁ x T₂/T₁

Or, V₂ = 4 L x 387 K/393 K = 3.94 L

Therefore

ΔV = V₂ – V₁ = 4 L – 3.94 L = 0.06 L

Problem 2: A balloon is filled to a volume of 3.2 L at a temperature of 25 ˚C. The balloon is then heated to a temperature of 65 ˚C. Assuming the pressure remains constant throughout, find the new volume of the balloon.

Solution:

Given

V₁ = 3.2 L

T₁ = 25 ˚C = 273 + 25 = 298 K

T₂ = 65 ˚C = 273 + 65 = 338 K

From Charles law,

V₁/T₁ = V₂/T₂

Or, V₂ = V₁ x T₂/T₁

Or, V₂ = 3.2 L x 338 K/ 298 K = 3.63 L