The Clausius-Clapeyron equation is fundamental in thermodynamics and establishes a relationship between the vapor pressure of a substance to its temperature. It provides a valuable understanding of the behavior of substances undergoing phase changes, such as melting and boiling ^[1-4].

The equation is named after German physicist and mathematician Rudolf Clausius and French engineer and physicist Benoît Paul Émile Clapeyron. They independently derived the equation in the mid-19th century.

Formula and Plots

The Clausius-Clapeyron equation states that the logarithm of the vapor pressure of a substance is directly proportional to its reciprocal absolute temperature. According to it, the natural logarithm of the liquid’s vapor pressure (P) is determined by the molar enthalpy of vaporization of the liquid (ΔH_vap), the ideal gas constant (R), and the temperature (T) of the system. Mathematically, the equation is represented by ^[4-6]

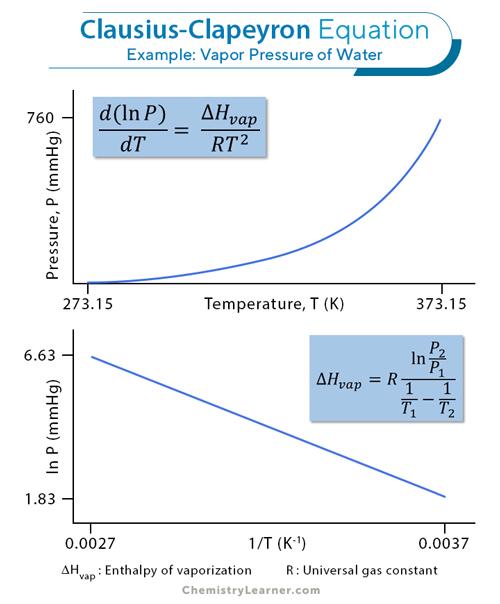
d (ln P)/ dT = ΔH_vap/RT²

Integrating the above equation and assuming that ΔH_vap does not depend on the system’s temperature, the Clausius-Clapeyron equation can be written in the following integrated form.

ln P = – ΔH_vap/RT + C

Where C is an arbitrary constant. This equation can be rewritten as

P = A exp (- ΔH_vap/RT)

Where A = exp (C). The plots of P vs. T and ln P vs. 1/T are shown below. 

To eliminate C from the above equation, we consider two points 1 and 2 on the ln P vs. 1/T plot that give two values of the vapor pressure and temperature – (P₁, T₁) and (P₂, T₂). Plugging these values, we get

ln (P₂/P₁) = (ΔH_vap/R) (1/T₁ – 1/T₂)

Rearranging the above equation, one can measure the molar enthalpy of vaporization of a liquid.

ΔH_vap = R((ln P₂ – ln P₁)/(1/T₁ – 1/T₂))

Derivation

The Clausius-Clapeyron equation is derived from thermodynamics principles. A substance goes from phase 1 to phase 2 during a phase transition. Along the phase boundary, the two phases are in equilibrium. Their specific Gibbs free energies (g) are equal ^[1,7-9].

g₁(p, T) = g₂(p, T)

Suppose there is a change of temperature from T to T + dT. The corresponding change in pressure is from P to P + dP. The Gibbs free energy of phase 2 will change by the same amount as that of phase 1.

dg₁ = dg₂

Since the specific Gibbs energy is a function of temperature and pressure, we can write dg as follows:

dg = (∂g/∂T)_P dT + (∂g/∂P)_T dP

However,

(∂g/∂T)_P = -s and (∂g/∂P)_T = v

Such that,

dg = -sdT + vdP

Therefore, the equilibrium condition becomes

-s₁dT + v₁dP = -s₂dT + v₂dP

=> -(s₁ – s₂)dT + (v₁ – v₂)dP = 0

=> dP/dT = (s₁ – s₂)/(v₁ – v₂)

The entropy change associated with the phase transition is

(s₁ – s₂) = (h₁ – h₂)/T = Δh/T

Where Δh is the latent heat. 

dP/dT = Δh/T(Δv)

The above expression is a generalized form of the Clausius-Clapeyron equation.

• When 1 = liquid and 2 = gas, Δh = ΔH_vap is the latent heat of vaporization
• When 1 = solid and 2 = liquid, Δh = ΔH_fus is the latent heat of fusion
• When 1 = solid and 2 = gas, Δh = ΔH_sub is the latent heat of sublimation

Consider the liquid-gas phase transition, occurring at temperatures much lower than the critical temperature of the substance. The specific volume of the gas phase greatly exceeds that of the liquid. 

v_g >> v_l and Δv = v_g

Then,

dP/dT = ΔH_vap/T(v_g)

At low temperatures and pressure, one may approximate the gas to follow the ideal gas law so that

v_g = RT/P

The Clausius-Clapeyron equation becomes

dP/dT = ΔH_vap/T(RT/P)

=> d(ln P)/dT = ΔH_vap/RT²

Uses and Applications

Applications of the Clausius-Clapeyron equation extend across diverse scientific disciplines, enabling one to make informed decisions regarding weather patterns, chemical reactions, and industrial processes involving phase changes ^[9-10].

• It helps meteorologists to understand cloud formation and precipitation patterns by relating temperature variations to changes in water vapor pressure.
• It aids chemists in determining reaction rates and equilibrium constants for reactions involving gases and volatile substances. 
• It assists engineers in designing efficient heat exchangers and distillation systems by considering how temperature affects vapor pressures during separation processes.