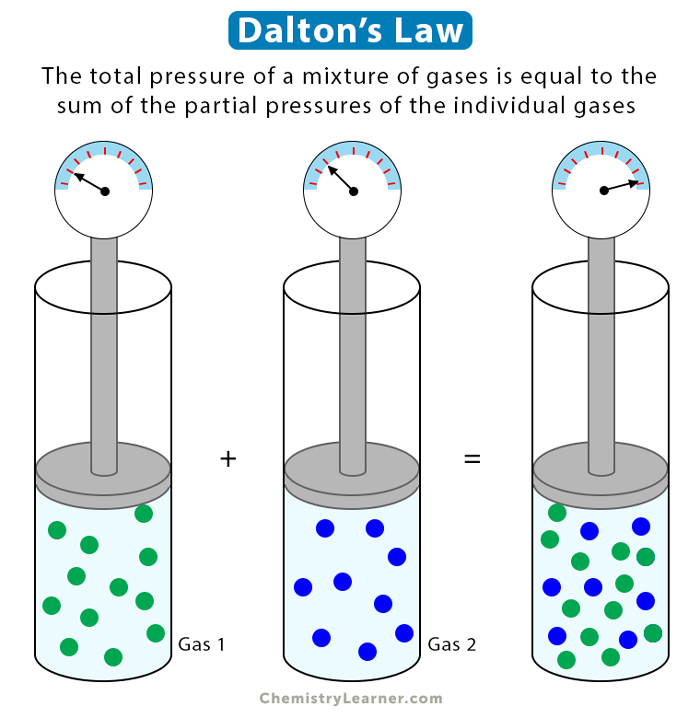
Dalton’s law of partial pressure states that in a mixture of two or more non-reacting gases, the sum of the partial pressures of each gas is equal to the overall pressure of the gas mixture. A gas’s partial pressure is the pressure it would exert on the walls if it were the only gas in a container ^[1-4].

English physicist and chemist John Dalton published the law in 1802.

Formula

For Dalton’s law to hold good, the following assumptions are made: ^[1-6]

• The gas molecules occupy an insignificant volume compared to the container’s volume.
• The gases are ideal, meaning there is no attraction among the molecules.
• The pressure is not excessively high. Otherwise, the volume occupied by the molecules becomes significant compared to the free space between them, resulting in a deviation from Dalton’s law.

Based on these assumptions, one can calculate the total pressure of the gas mixture in terms of the partial pressure of the gases. Suppose a mixture contains n gases whose partial pressures are p₁, p₂, p₃, …, p_n. Then, the total pressure p of the mixture is given by

p = p₁ + p₂ + p₃ + … + p₄

p = Σp_i

Partial Pressure from Mole Fraction

Dalton’s law can also be expressed in terms of mole fraction. The mole fraction X is the fraction of the gas present in the mixture. It is evaluated by taking the ratio of the number of moles (n_i) of a given gas and the total number of moles (Σn_i) of all the gases.

 X_i = n_i /(Σn_i)

Then, the partial pressure of the i-th gas is

p_i = X_i p

Partial Pressure from Ideal Gas Equation

The partial pressure can be calculated from the ideal gas equation. Suppose n_i moles of the i-th gas are present in the mixture. The partial pressure is given by

p_i = n_iRT/V

Where

T: Absolute temperature

V: Volume of the gas

Solved Problems

Problem 1: A mixture of oxygen and hydrogen exerts a total pressure of 2.3 atm on the walls of the container. If the partial pressure of hydrogen is 1.2 atm, find the mole fraction of oxygen in the mixture.

Solution:

Given,    p_hydrogen = 1.2 atm             p = 2.3 atm        

Therefore, the partial pressure of oxygen is

p_oxygen = p – p_hydrogen = 2.3 atm – 1.2 atm = 1.1 atm

The mole fraction of oxygen can be found using the following formula.

p_oxtgen = X_oxygen p

=> X_oxygen = p_oxygen/p

=> X_oxygen = 1.1 atm/2.3 atm = 0.48

Problem 2: 14 L of oxygen gas at 2.4 atm and 18 L of nitrogen at 2.2 atm are added to a 12 L container at 300 K. Find the partial pressure of oxygen and nitrogen and then find the total pressure.

Solution:

Given    V_oxygen = 14 L       p_oxygen¹ = 2.4 atm              V_nitrogen = 18 L     p_nitrogen¹ = 2.2 atm             T = 300 K

V = 12 L               R = 0.082 L-atm · mol^-1 · K^-1

The mole fraction of oxygen is

n_oxygen = (p_oxygen V_oxygen)/(RT) = (2.4 atm · 14 L)/(0.082 L-atm · mol^-1 · K^-1 · 300 K) = 1.36 mol

n_nitrogen = (p_nitrogen V_nitrogen)/(RT) = (2.2 atm · 18 L)/(0.082 L-atm · mol^-1 · K^-1 · 300 K) = 1.61 mol

Therefore, the total number of moles is

n = n_oxygen + n_nitrogen = 1.36 + 1.61 = 2.97 mol

The total pressure is

P = nRT/V = 2.97 mol · 0.082 L-atm · mol^-1 · K^-1 · 300 K/12 L = 6.09 atm

Therefore, the partial pressures are

p_oxygen = (n_oxygen/n) · P = (1.36 mol/2.97 mol) · 6.09 atm = 2.78 atm

p_nitrogen = (n_nitrogen/n) · P = (1.61 mol/2.97 mol) · 6.09 atm = 3.3 atm