Effective Nuclear Charge
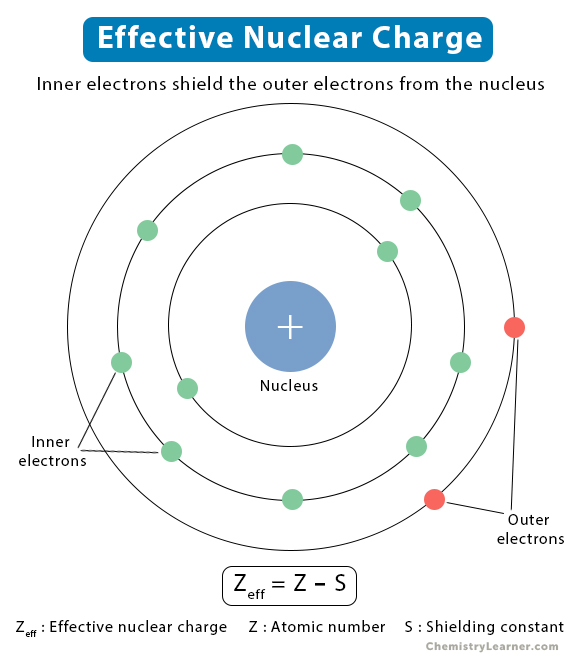
An atom consists of the nucleus surrounded by electrons residing in different shells. Electrostatic forces of attraction arise between the nucleus and the electrons. Similarly, electrostatic repulsive forces also arise between the inner and the outer electrons. The repulsive forces weaken the attractive forces, resulting in electron shielding [1,2].
What is Effective Nuclear Charge
According to Coulomb’s law, the attractive electrostatic force between the nucleus and the electron depends on the nuclear charge, electron charge, and electron-nucleus distance. However, Coulomb’s law is only suitable for single-electron atoms or ions. For a multi-electron atom, the calculations are complicated as the forces need to be added vectorially. Overall, the outer electrons experience a lower force and a reduced nuclear charge due to shielding by the inner electrons. This reduced charge is known as the effective nuclear charge. It is called effective because the shielding prevents the outer electrons from experiencing the full charge [1-4].
Effective Nuclear Charge and Nuclear Charge
The actual nuclear charge is the atomic number multiplied by the proton charge. On the other hand, the effective nuclear charge is the net charge on the nucleus that attracts the valence electrons towards itself. The effective nuclear charge is always less than the actual nuclear charge [3].
Effective Nuclear Charge Equation
The effective nuclear charge can be approximated as [1],
Zeff = Z – S
Where,
Zeff: Effective nuclear charge
Z: Atomic number
S: Shielding constant
How to Find the Effective Nuclear Charge
The effective nuclear charge can be determined by using Slater’s rule. This rule calculates Zeff from the actual number of protons in the nucleus and the effect of electron shielding. In order to illustrate this concept, let us take the example of chlorine (Z = 17), whose electron configuration is 1s22s22p63s23p5 [5].
Step 1: Arrange the electron configuration according to the following subshells.
(1s) (2s, 2p) (3s, 3p) (3d) (4s, 4p) (4d) (4f) (5s, 5p) …
For chlorine, the arrangement is as follows.
(1s2) (2s2, 2p6) (3s2, 3p5)
Step 2: Identify the electron of interest. It can be an inner or outer electron.
Let us choose a 3p-electron of chlorine.
Step 3: Find the shielding experienced by electrons in different subshells. Divide it into two parts.
Part 1: For s- or p-electron
- Electrons in the same n group shield 0.35, except the 1s electron, which shield 0.30
- Electrons in the (n-1) group shield 0.85
- Electrons in the (n-2) and lower groups shield 1.00
Part 2: For d- and f-electron
- Electrons in the same n group shield 0.35
- Electrons in the lower n group shied 1.00
In the case of chlorine,
- 6 electrons are in n = 3 group: 6 x 0.35 = 2.1
- 8 electrons are in the n = 2 group: 8 x 0.85 = 6.8
- 2 electrons are in the n = 1 group: 2 x 1.00 = 2
Therefore, the shielding constant is given by,
S = 2.1 + 6.8 + 2 = 10.9
Hence, the effective nuclear charge experienced by a 3p-electron of chlorine is,
Zeff = 17 – 10.9 = 6.1
Effective Nuclear Charge Periodic Trend
The effective nuclear charge increases across a period in the periodic table. The reason is that the atomic number increases across a period, thereby increasing the nuclear charge. However, there is no extra shell of electrons to increase the shielding constant [6].
The effective nuclear charge decreases down a group. The reason is that there is an extra shell of electrons for every period down a group. This effect is so prominent that it counters the effect due to the increasing atomic number.
Problems
P.1. Determine the effective nuclear charge of lithium (Z = 3).
Soln.:
Step 1: The electronic configuration of lithium is,
(1s2) (2s1)
Step 2: The electrons of interest are 1s- and 2s-electrons.
Step 3: For 1s-electrons: 1 x 0.3 = 0.3
Hence,
Zeff = 3 – 0.3 = 2.7
For 2s-electron: 2 x 0.85 = 1.7
Hence,
Zeff = 3 – 1.7 = 1.3
| Z | 3 |
| 1s | 2.7 |
| 2s | 1.3 |
P.2. Determine the effective nuclear charge of F– (Z = 9).
Soln.:
Step 1: Fluoride (F–) has 10 electrons, of which 2 are inner and 8 are outer. Its electron configuration is,
(1s2) (2s2, 2p6)
Step 2: The electron of interest is a valence electron or a n = 2 electron.
Step 3: The shielding constant is calculated as follows.
7 electrons in the same n = 2 group: 7 x 0.35 = 2.45
2 electrons in the n = 1 group: 2 x 0.85 = 1.7
Therefore, S = 2.45 + 1.7 = 4.15
Hence, Zeff = 9 – 4.15 = 4.85