All gases show similar behavior under ordinary conditions. Gas laws are a set of empirical laws that describes this behavior. They establish a relationship between the following properties ^[1-4]:

• Pressure
• Volume
• Temperature
• Number of moles

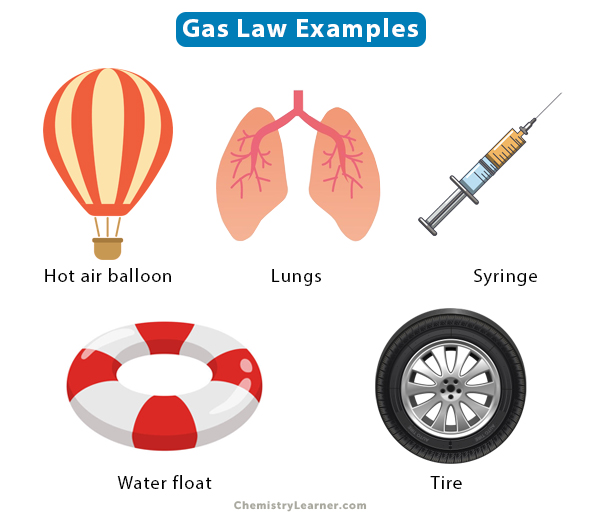
The gas laws were developed by several scientists after whom they have been named. They are important in real and everyday life. For example, pumping air in a balloon, water floats, and car tires must obey gas laws.

List of Gas Laws

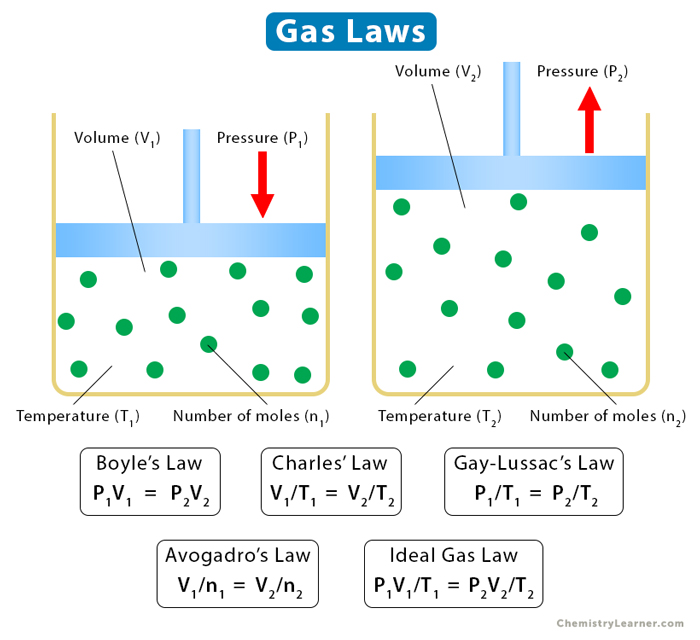
There are five gas laws, and they are discussed below ^[1-8].

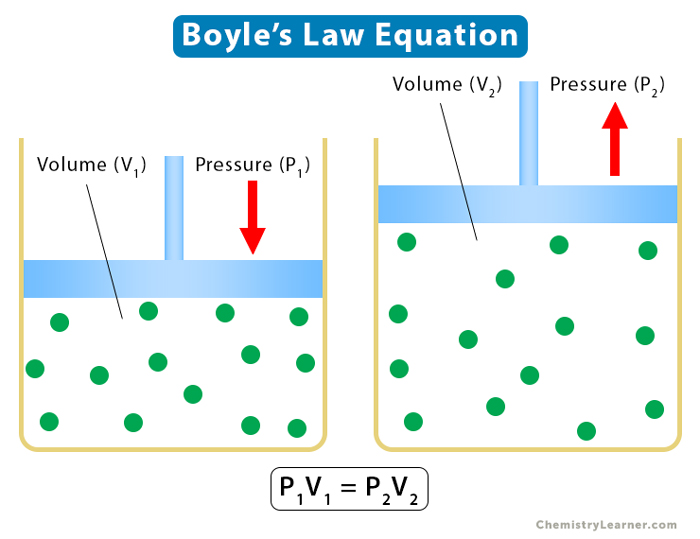
1. Boyle’s Law

Boyle’s law establishes a relationship between pressure and volume, keeping temperature and the number of moles constant. According to it, the pressure is inversely proportional to the volume.

Equation

Suppose P is the pressure and V is the volume, then

P ∝ 1/V

The following relationship holds for two different states of a gas defined by (P₁, V₁) and (P₂, V₂).

P₁V₁ = P₂V₂

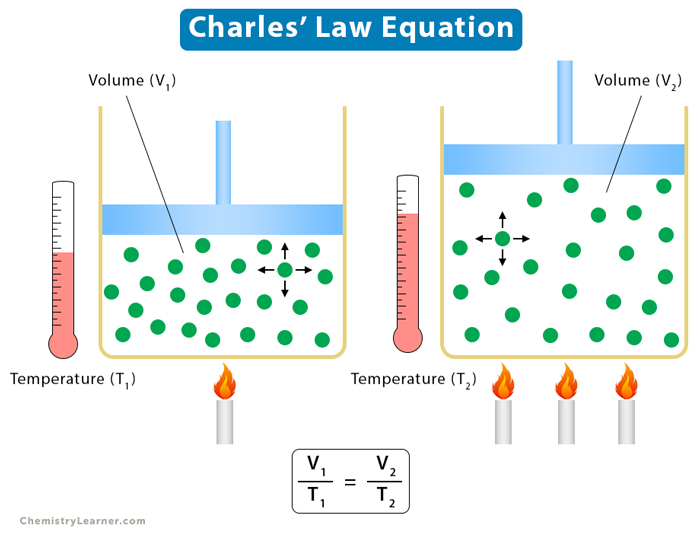
2. Charles’ Law

Charles’ law establishes a relationship between volume and temperature, keeping pressure and the number of moles constant. According to it, the volume is proportional to temperature.

Equation

Suppose V is the volume and T is the temperature. Then,

V ∝ T

The following relationship holds for two different states of a gas defined by (V₁, T₁) and (V₂, T₂).

V₁/T₁ = V₂/T₂

3. Gay-Lussac’s Law

Gay-Lussac’s law establishes a relationship between pressure and temperature, keeping the volume and number of moles constant. According to it, the pressure is directly proportional to the temperature.

Equation

Suppose P is the pressure and T is the temperature. Then,

P ∝ T

The following relationship holds for two different states of a gas defined by (P₁, T₁) and (P₂, T₂).

P₁/T₁ = P₂/T₂

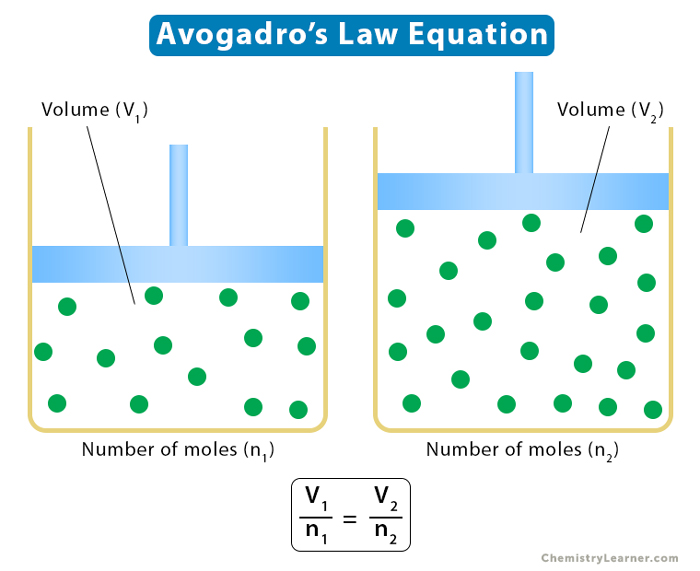
4. Avogadro’s Law

Avogadro’s law states that equal volumes of different gases contain an equal number of molecules, provided the temperature and volume are kept constant. It establishes a relationship between volume and the number of moles. The number of moles represents the mass of the gas. According to this law, the volume is directly proportional to the number of moles.

Equation

Suppose V is the volume and n is the number of moles. Then,

V ∝ n

Suppose a gas goes from one state to another such that its volume changes from V₁ to V₂. The number of moles changes from n₁ to n₂. Then, the following relationship holds.

V₁/n₁ = V₂/n₂

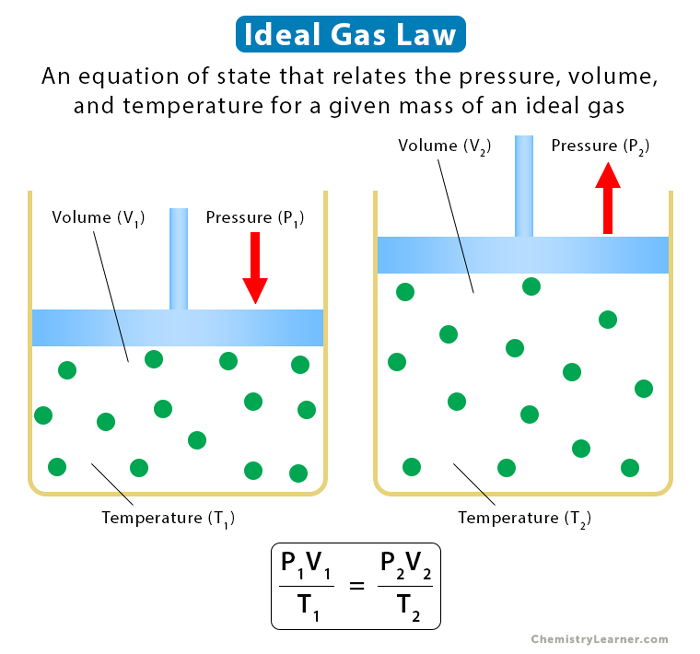
5. Ideal Gas Law

Ideal gas law combines the above four laws. It establishes a relationship between pressure, volume, temperature, and the number of moles.

Equation

Suppose P is the pressure, V is the volume, T is the temperature, and n is the number of moles. Then,

PV = nRT

The following relationship holds for gas with a constant number of moles going from one state (P₁, V₁, T₁) to another state (P₂, V₂, T₂).

P₁V₁/T₁ = P₂V₂/T₂

The following image and table summarize all the gas laws.

Name of the Gas Law	Variable	Constant	Equation
Boyle’s Law	Pressure (P) and Volume (V)	Temperature (T) and number of moles (n)	PV = constant
Charles’ Law	V and T	P and n	V/T = constant
Gay-Lussac’s Law	P and T	V and n	P/T = constant
Avogadro’s Law	V and n	P and V	V/n = constant
Ideal Gas Law	P, V, n, and T	None	PV = nRT

The following image shows a few examples of where gas laws are applied.

Problems and Solutions

Problem 1: 5.5 L of an ideal gas are contained at 2.0 atm pressure and 27 °C. How many moles of the gas are present? (R = 0.082 L·atm·M^-1·K^-1)

Solution:

Given,

V = 5.5 L

P = 2.0 atm

T = 27 ˚C = 273 + 27 = 300 K

R = 0.082 L·atm·M^-1·K^-1

From ideal gas equation,

PV = nRT

Or, n = PV/RT

Or, n = (2.0 atm x 5.5 L)/(0.082 L·atm·M^-1·K^-1 x 300 K)

Or, n = 0.45

Problem 2: A 350 mL can of hair spray is used until it is empty, except for its propellant gas. The gas in the can is initially at 18 °C and 420 kPa. What is the new pressure in the can if it is left in a car that reaches 45 °C on a hot day?

Solution:

Given

P₁ = 420 kPa

T₁ = 18 ˚C = 18 + 273 = 291 K

T₂ = 45 ˚C = 45 + 273 = 318 K

From Gay-Lussac’s law,

P₁/T₁ = P₂/T₂

Or P₂ = P₁T₂/T₁

Or, P₂ = 420 kPa x 318 K/291 K

Or, P₂ = 459 k Pa