Gibbs’ Phase Rule is crucial in thermodynamics, where it enables scientists to analyze and predict the equilibrium conditions of a system based on its components and phases. By providing a systematic approach to understanding the interplay between variables, Gibbs’ Phase Rule facilitates the exploration of various thermodynamic scenarios, from simple single-phase systems to more complex, multi-component systems. This understanding is vital for theoretical research and practical applications in materials science, chemical engineering, and environmental science. ^[1-4]

American physicist Josiah Willard Gibbs developed this rule in the 1870s.

Significance

Gibbs Phase Rule’s significance becomes particularly evident when dealing with systems undergoing phase transitions, where different states of matter coexist. It helps researchers decipher the conditions under which these phase changes occur and the factors influencing the equilibrium state. Gibbs’ Phase Rule allows for a quantitative assessment of the degrees of freedom within a system, revealing the number of independent variables that can be altered without affecting the system’s equilibrium. In other words, the rule offers a quantitative understanding of the relationships among the number of components, phases, and degrees of freedom within a given system.

Degrees of freedom quantify the extent to which a system can evolve while maintaining equilibrium. In a physical system, the degrees of freedom indicate the number of ways energy can be distributed among the system’s components. Understanding degrees of freedom is crucial for predicting and analyzing the behavior of complex systems undergoing phase transitions. ^[1]

Key Variables

Several key variables come into play in the Gibbs’ Phase Rule context. Components are the chemically independent constituents of the system, influencing its overall behavior. Phases are distinct, physically separable forms of matter within the system, such as solid, liquid, or gas. The crucial concept of degrees of freedom encapsulates the number of intensive variables, like temperature and pressure, that can be independently varied without disturbing the equilibrium. Understanding these variables is essential to applying Gibbs’ Phase Rule effectively and comprehending the intricate relationships governing the equilibrium of multi-component, multi-phase systems. ^[1-7]

The interplay of components, phases, and degrees of freedom is intricately linked to the equilibrium conditions within a system. Gibbs’ Phase Rule is expressed mathematically as:

F = C – P + 2

Where:

• F represents the degrees of freedom.
• C is the number of components.
• P is the number of phases.

This relationship captures the constraints and dependencies among these variables, elucidating the equilibrium state of a system. As the degrees of freedom decrease, the system becomes more constrained and approaches a state of equilibrium, providing a powerful tool for predicting and understanding the behavior of complex systems in various scientific disciplines, from chemistry to material science and beyond.

Examples

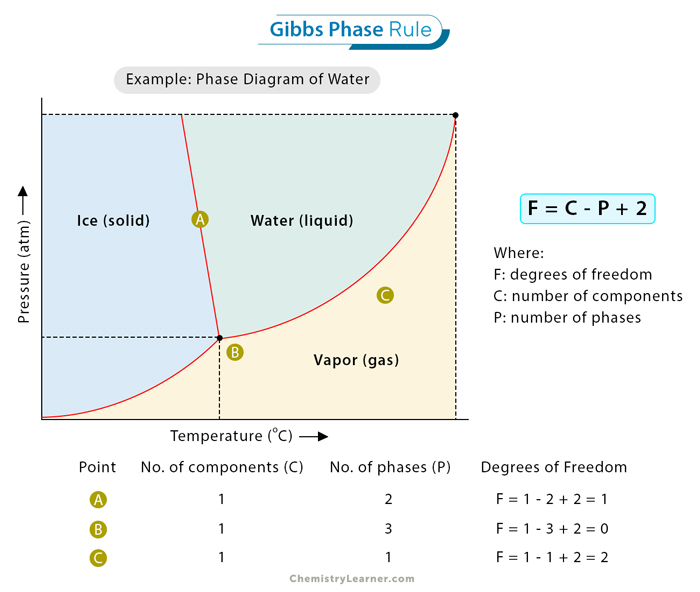
Let us consider a practical example to illuminate the application of Gibbs’ Phase Rule. Imagine a system containing water, ice, and water vapor in equilibrium, as shown in the image. In this scenario, the components are water molecules, and the phases are liquid water, solid ice, and gaseous water vapor. Applying the phase rule to this system involves understanding the constraints and variables. ^[1,2]

For this example, the phase rule equation can determine one component (water molecules), three phases (solid, liquid, and gas), and an unknown number of degrees of freedom. In the diagram, three points, A, B, and C are chosen.

At point A, C = 1, P = 2, and F = 1 – 2 + 2 = 1.

At point B, C = 1, P = 3, and F = 1 – 3 + 2 = 0.

At point C, C = 1, P = 1, and F = 1 – 1 + 2 = 2.

At point A, F = 1. The system has one degree of freedom, typically represented by temperature. It means that while the pressure and temperature can vary independently, they are interrelated, and changes in one variable will impact the other to maintain equilibrium.

At point B, F = 0. There are no degrees of freedom. It means the system is fully constrained in equilibrium. The temperature and pressure are both fixed, and this point is called the triple point of water.

Derivation

The Gibbs’ phase rule is derived by considering that the count of independent variables is determined by subtracting the constraints from the total number of variables. It includes temperature, pressure, and all necessary variables to characterize each phase. The derivation involves a systematic breakdown of the relationships between the number of components, phases, and degrees of freedom in a given system. ^[1,2,6]

C-1 variables characterize the composition of each phase within a system. Considering there are P phases in a system, the number of compositional variables is then P(C−1), which is calculated by multiplying the number of phases by the variables per phase. The overall number of variables within the system is expressed as P(C−1) + 2, accounting for compositional variables and adding one variable each for pressure and temperature.

The degrees of freedom in the system are calculated as the difference between the total number of variables and the variables specified by establishing equilibrium conditions. A prerequisite for equilibrium is that the chemical potential of each component is uniform across all phases. With P−1 independent equations for each component in every phase, specifying equal chemical potentials for all combinations of phases, except one, implies their equality in the remaining pair of phases. This dependent equation is constructed from others and is not considered.

In a system in equilibrium, C(P−1) variables are specified (P−1 for each component, multiplied by the number of components). Therefore, the expression for degrees of freedom is:

F = P(C-1) + 2 – C(P-1)

Simplifying, we arrive at

F = C – P + 2

which is the Gibbs’ Phase Rule.