The Henderson-Hasselbalch equation is an equation used in chemistry and biochemistry to determine the pH value of a buffer solution during the dissociation of a weak acid. A weak acid does not dissociate completely. A property of the buffer solution is that the mixture can resist changes in pH when a small amount of acid is added ^[1-5].

How to Use Henderson Hasselbalch Equation

The Henderson-Hasselbalch equation is used to determine the amount of acid and conjugate base needed to make a buffer solution of a certain pH. Therefore, it is often used to perform the calculations necessary to prepare buffers for use in the laboratory or other applications.

General Formula of the Henderson-Hasselbalch Equation

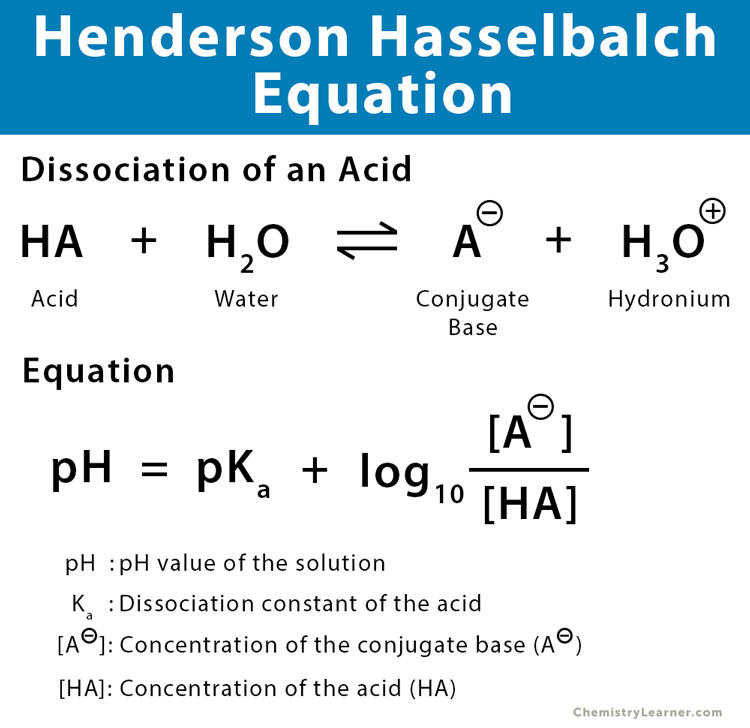
A simple buffer solution consists of a weak acid solution and a salt of the acid’s conjugate base. The equation is given by,

pH = pK_a + log₁₀[conjugate base/weak acid]

where,

pH: pH value

K_a: acid dissociation constant

[conjugate base]: Concentration of the conjugate base in moles per liter

[weak acid]: Concentration of the acid in moles per liter

American chemist Lawrence Joseph Henderson first derived the equation in 1908 and, later, by Danish chemist Karl Albert Hasselbalch in 1917.

Derivation of Henderson-Hasselbalch Equation

The Henderson-Hasselbalch equation can be derived from the equilibrium constant expression for the dissociation of a weak acid. Consider the dissociation of the acid HA in water H₂O ^[2-6].

HA + H₂O ⇄ A^– + H₃O⁺

The acid dissociation constant is given by,

K_a = [A^–] [H₃O⁺]/[HA]

or, [H₃O⁺] = K_a[HA]/ [A^–]

or, log₁₀ [H₃O⁺] = log₁₀ (K_a[HA]/ [A^–])

or, log₁₀ [H₃O⁺] = log₁₀ K_a + log₁₀ ([HA]/[A^–])

or, – log₁₀ [H₃O⁺] = – log₁₀ K_a – log₁₀ ([HA]/[A^–])

or, pH = pK_a + log₁₀ ([A^–]/[HA])

From the above equation, the following points can be noted.

1. The value of [A^–]/[HA] is dependent on the values of the pH and pK_a.

• When pH < pK_a, [A^–]/[HA] < 1.
• When pH > pK_a, [A^–]/[HA] > 1.

2. When the pH changes relatively to pK_a by one unit, then pH – pK_a = 1. Therefore,

1 = log₁₀ ([A^–]/[HA])

or, [A^–]/[HA] = 10

Thus, the ratio of the dissociated form to the associated form changes by a factor of 10.

3. When the acid is 50% dissociated, the acid and the conjugate base concentrations are the same.

[HA] = [A^–]

or, [HA]/[A^–] = 1

Therefore,

pH = pK_a

The pH value of the solution is equal to the pK_a value of the acid.

Henderson-Hasselbalch Equation for Base

The Henderson-Hasselbalch equation also applies to a weak base. A weak base dissociates as follows,

B + H₂O  ⇄  OH^– + HB⁺

The Henderson-Hasselbalch equation can be derived using the same principles as that for acid and gives,

pOH = pK_b + log₁₀ ([HB⁺]/[B])

where,

pOH: pOH value

K_b: base dissociation constant

[HB⁺]: Concentration of the conjugate acid in moles per liter

[B]: Concentration of the base in moles per liter

Limitations of Henderson-Hasselbalch Equation

• Fails to predict the pH values of strong acids because it assumes that the acid and its conjugate base concentrations remain constant at equilibrium.
• Can only be applied to a polybasic acid if its consecutive pK values differ by at least 3.
• Fails to give an accurate pH value for extremely buffer solutions.
• Does not consider the self-dissociation by water.

Examples and Problems

P.1. The dissociation of acetic acid (CH₃CO₂H) in acetate ion (CH₃CO₂⁻) is given as follows:

CH₃CO₂H + H₂O  ⇄  CH₃CO₂⁻ + H₃O⁺

Calculate the pH of a buffer solution made from 0.25 M of CH₃CO₂H and 0.45 M of CH₃CO₂⁻ that has an acid dissociation constant for CH₃CO₂H of 1.76 x 10^-5 at 25  ͦC.

Soln. Given,

[CH₃CO₂H] = 0.25 M

[CH₃CO₂⁻] = 0.45 M

K_a = 1.76 x 10^-5

The Henderson-Hasselbalch equation is given by,

pH = pK_a + log₁₀ ([A^–]/[HA])

Therefore,

pH = -log₁₀ (1.76 x 10^-5) + log₁₀ (0.45 M /0.25 M) = 5

P.2. How much sodium formate (HCOONa), 68.0069 g/mol) do you need to add to 500 mL of 0.50 M formic acid (HCOONa) for a pH 3 buffer. K_a = 1.77 x 10¯⁴.

Soln. Given,

[HCOONa] = 0.5 ML^-1

pH = 3

K_a = 1.77 x 10¯⁴

The Henderson-Hasselbalch equation is given by,

pH = pK_a + log₁₀ ([A^–]/[HA])

Therefore,

3 = – log₁₀ (-1.77 x 10¯⁴) + log₁₀ ([A^–]/0.5)

or, 3 = 3.752 + log₁₀ ([A^–]/0.5)

or, log₁₀ ([A^–]/0.5) = -0.752

or, [A^–]/0.5 = 0.177

or, [A^–] = 0.177 x 0.5 = 0.0885 ML^-1

The relationship between the concentration and the molecular weight is,

Concentration x volume = weight/molecular weight

0.0885 ML^-1 x 0.5 L = w/ 68.0069 gM^-1

Or, w = 0.0885 ML^-1 x 0.5 L x 68.0069 gM^-1 = 3 g