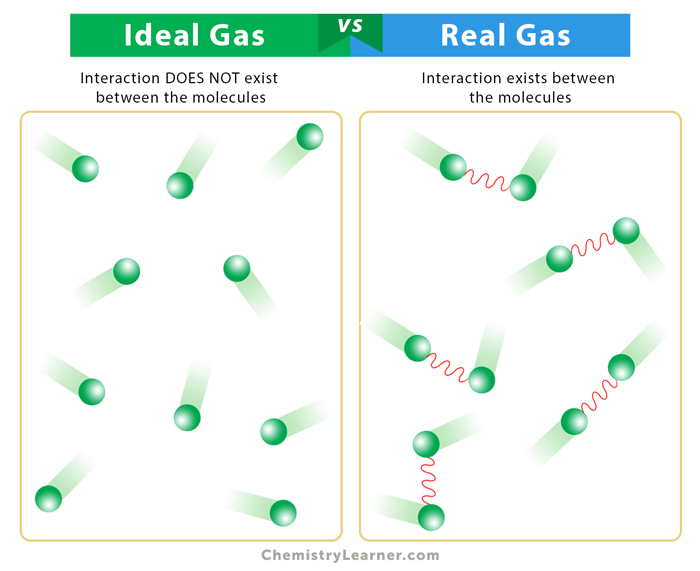
An ideal gas is one where the collisions between the molecules are perfectly elastic, and no intermolecular forces exist between them. The ideal gas law is a law that explains the state of an ideal gas. It establishes a relationship between macroscopic properties like pressure, volume, temperature, and the number of moles. Many gases like hydrogen, oxygen, nitrogen, and carbon dioxide can be treated as ideal gases ^[1-4].

The ideal gas law was first proposed by French engineer and physicist Emile Clapeyron in 1834 to combine the fundamental laws of physical chemistry.

Characteristics of an Ideal Gas

We make a few assumptions to characterize an ideal gas ^[1,2].

• The volume of the gas molecules is negligible. In other words, the volume is much smaller than the container’s volume.
• The gas molecules are of equal size and do not interact.
• The gas molecules move randomly and follow Newton’s law.
• The collisions among the gas molecules are perfectly elastic without any energy loss.

Ideal Gas Equation

To derive the ideal gas equation, we combine the three basic gas laws: Boyle’s law, Charles’ law, and Avogadro’s law. Suppose a gas consisting of n moles is at a pressure P, volume V, and temperature T. Then, the following relationships arise from these three gas laws ^[1-5].

From Boyle’s law,

P ∝ 1/V

From Charles’ law,

V ∝ T

From Avogadro’s law,

V ∝ n

Combining the above three laws

V ∝ nT/P

Or, PV = nRT

Where

P : Pressure

V : Volume

T : Temperature

n : Number of moles

R : Ideal gas constant

The constant of proportionality R is known as the ideal gas constant or universal gas constant. Its value is 8.314 J·M^-1·K^-1 or 0.0082 atm·L·M^-1·K^-1.

The above equation is the ideal gas equation. The pressure, volume, and temperature units must be consistent. Pressure is expressed in pascal (Pa) or atmosphere (atm), volume is expressed in m³ or liter (L), temperature is expressed in Kelvin (K), and the number of miles is expressed as M. The right-hand side of the equation has the unit of energy. It means that the energy is related to the pressure and volume of the gas.

Alternative Form

The ideal gas equation can be written in terms of Boltzmann’s constant. Let us write the number of moles in terms of the number of molecules (N) and Avogadro’s number (N_A).

n = N/N_A

Then, the ideal gas equation becomes

PV = (N/N_A)RT

Or, PV = Nk_BT

Where k_B=R/N_A is called Boltzmann’s constant. It has a value of 1.38 x 10^-23 J·K^-1.

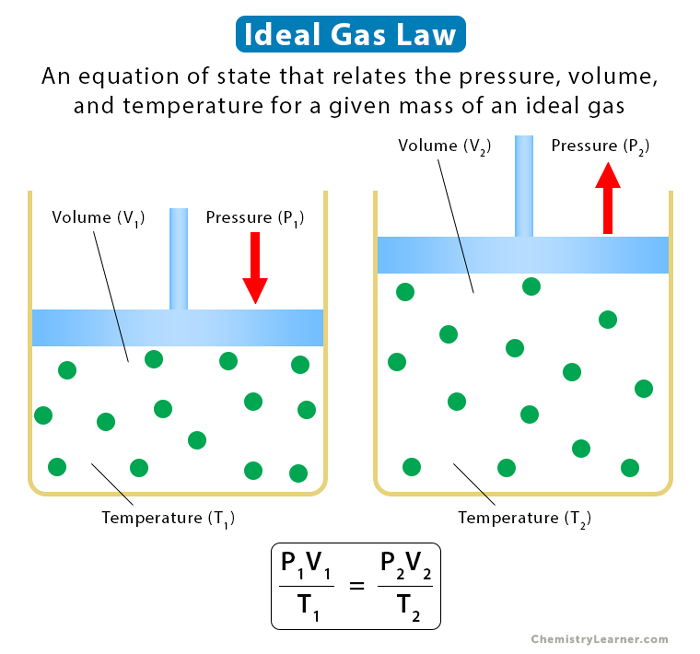
Relationship Between Different States

The ideal gas equation can be used to establish the relationship between two different states of gas. Rewriting it as

PV/T = nR

As long as the number of moles remains constant, the term PV/T is constant. Suppose a process starts from state 1 with pressure P₁, volume V₁, and temperature T₁. It goes to state 2 with pressure P₂, volume V₂, and temperature T₂. Then, irrespective of how the process occurred, the following relationship holds.

P₁V₁/T₁ = P₂V₂/T₂

Standard Temperature and Pressure (STP)

Specific temperature and pressure values are chosen as reference points, known as standard temperature and pressure (STP). These values are P = 1 atm or 100 kPa and T = 0 ˚C or 273 K. Using these values in the ideal gas equation, we can calculate the volume of one mole of an ideal gas.

PV = nRT

Or, V = nRT/P

Or, V = 1 M x 0.082 L·atm·M^-1·K^-1 x 273 K/1 atm

Or, V = 22.5 L

Density and Molar Mass

The ideal gas equation can determine the density and molar mass. Rewriting it as

n/V = P/RT

The number of moles is given by the total mass (m) divided by its molecular mass (M).

n = m/M

Therefore,

m/MV = P/RT

Or, ρ = MP/RT

Where ρ = m/V is the density of the gas.

The distance of separation between the gas molecules is much more than the molecules’ size. Hence, the density is very compared to solids and liquids.

Ideal Gas vs. Real Gas

A real gas is one whose molecules occupy space and have intermolecular interactions. Consequently, they do not obey the ideal gas law. The following table compares ideal gas to real gas.

	Ideal Gas	Real Gas
Molecular size	Small	Large
Collision	Elastic	Inelastic
Intermolecular forces	None	Exist
Pressure	High	Low
Equation	PV = nRT	(P + an2)/V2 = (V-nb)nRT

Example Problems and Solutions

Problem 1: 3 moles of carbon dioxide gas is in an 80-liter fixed cylinder at 320 Kelvin. What is the pressure of the gas?

Solution:

Given

n = 3

V = 80 L

T = 320 K

From the ideal gas equation,

PV = nRT

Or, P = nRT/V

Or, P = 3 M x 0.082 L·atm·M^-1K^-1 x 320 K/80 L

Or, P = 0.984 atm

Problem 2: Determine the volume occupied by 10 grams of nitrogen gas at STP.

Solution:

Molecular mass of nitrogen (M) = 28 g

Volume occupied by 28 grams of nitrogen at STP = 22.4 L

Therefore, volume occupied by 10 g of nitrogen = 22.4 L/28 g x 10 g = 8 L

FAQs