A thermodynamic process that maintains a constant entropy for a fluid or gas is called an isentropic process. It is a specific case of an adiabatic process where there is no exchange of heat or matter, and the entropy change is zero. For an irreversible adiabatic process, the entropy increases; hence, the entropy change is not zero. Heat is removed from the system for a reversible adiabatic process to keep the entropy constant. Therefore, the isentropic process is synonymous with the reversible adiabatic process ^[1-4].

The isentropic process is helpful in engineering because it is an idealized process that can be used for comparisons to all real processes. It often occurs in almost all known thermodynamic cycles like the Carnot Cycle, Otto Cycle, Diesel Cycle, Brayton Cycle, and Rankine Cycle.

Isentropic Relations

An isentropic transformation is carried out for reversible processes by thermally insulating the system from its surroundings. The following section discusses the various thermodynamic properties.

1. Isentropic process follows adiabatic gas law.

PVⁿ = constant

Where P is the pressure, V is the volume, and n is the adiabatic gas constant.

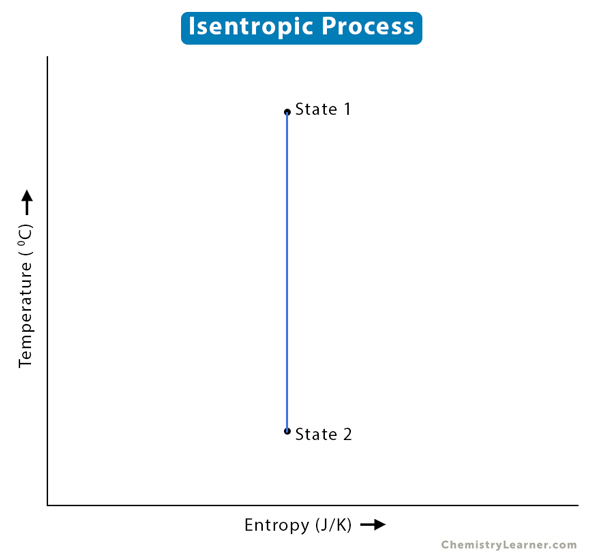
If the gas goes from state 1 to state 2, then

P₁V₁ⁿ = P₂V₂ⁿ

(T₂/T₁) = (V₁/V₂)^n-1

(T₂/T₁) = (P₁/P₂)^(n-1)/n

2. Heat transferred (ΔQ) is zero.

ΔQ = 0

3. The change in entropy (ΔS) is zero.

ΔS = 0

4. The change in internal energy (ΔU ) is given by the product of mass (m), specific heat at constant volume (c_v), and temperature change (ΔT).

ΔU = mc_v(T₂ – T₁)

5. The change in enthalpy (ΔH) is given by the product of mass (m), specific heat at constant pressure (c_p), and temperature change (ΔT).

ΔH = mc_p(T₂ – T₁)