An isobaric process is a thermodynamic process that takes place at constant pressure. The term isobaric originates from two Greek words – iso, meaning equal, and baros meaning pressure ^[1-4].

Examples

Suppose an ideal gas is confined to a container. Constant pressure is achieved by allowing its volume to expand or contract when heat is transferred between the gas and the surroundings. Any change in pressure is adjusted by changing the volume. This process of expansion and contraction is illustrated in the given diagram of a weighted piston ^[1-4].

Some other examples of isobaric processes in real life are:

• During boiling water to steam or freezing water to ice, water either expands or contracts to maintain constant pressure. The heat supplied during boiling increases the temperature and does external work.
• The operations of heat engines often involve isobaric processes. Heat engines operate on thermodynamic cycles that take heat from a hot reservoir, reject heat to a cold reservoir, and perform valuable work. Specific steps in the Brayton and Rankine cycles take place under isobaric conditions.

Heat Transfer in an Isobaric Process

Isobaric processes can be further understood using the first law of thermodynamics. It gives a relationship between the heat transfer (Q) between the system and the surroundings, the internal energy change (ΔU) in the system, and the work done (W). The mathematical representation of the first law is ^[1-4]

ΔU = Q – W

The work done is given by the product of pressure (p) and change in volume (ΔV). It is known as boundary work.

W = pΔV

A detailed explanation of the work done is discussed in the next section.

A part of the transferred heat will change the internal energy. Therefore, we use the system’s enthalpy change to determine the heat. The enthalpy (H) is given by

H = U + pV

Or, ΔH = ΔU + pΔV +VΔp

Putting this in the classical expression of the first law, we get

ΔH = Q – pΔV + pΔV +VΔp

or, ΔH = Q + VΔp

For an isobaric process, Δp = 0.

ΔH = Q

or, Q = (H₂ – H₁)

Therefore, the heat transferred is the change in the system’s enthalpy. The above equation is the isobaric form of the first law. It is calculated for open systems.

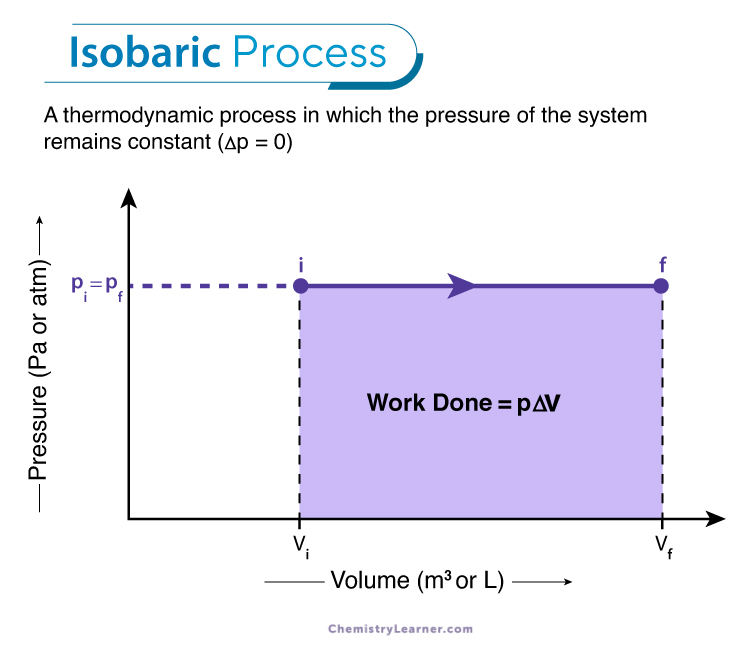
Work Done in an Isobaric Process

The work done in an isobaric process can be calculated from the P-V diagram. A P-V diagram is a graphical representation of the relationship between the pressure and the volume. Since the pressure remains constant in an isobaric process, the P-V diagram is a straight line parallel to the volume axis, as shown below. ^[1-4]

The work done is given by integrating the area under the p-V line.

W = ∫pdV

or, W = p ΔV

or, W = p (V_f -V_i)

Where

V_i: initial volume of the gas

V_f: final volume of the gas

The expansion or contraction of the gas in an isobaric process is accompanied by a change in temperature. It is often convenient to calculate the work in terms of the temperature since the latter can be measured easily. We will use the ideal gas equation below for this purpose.

PV = nRT

Where

n: number of moles of the gas

R: universal gas constant

At constant pressure, we can write the above equation as

pΔV = nRΔT

Or, p(V_f – V_i) = nR(T_f – T_i)

Or, W = nR(T_f – T_i)

Where,

T_i: initial temperature of the gas

T_f: final temperature of the gas

Sign Convention

Recall the expression for work done when the gas expands or contracts.

W = p ΔV

The sign of work done depends on whether ΔV can be positive or negative. Consequently, there can be two outcomes. ^[1]

• When the gas expands, its final volume is greater than the initial volume, i.e., V_f >V_i. Therefore, ΔV > 0 and W > 0. It means that the work done by the gas is positive.
• When the gas contracts, its final volume is less than the initial volume, i.e., V_f < V_i. Therefore, ΔV < 0 and W < 0. It means that the work done by the gas is negative.

Example Problems

Problem 1: 2 m³ volume of an ideal gas is stored under a constant pressure of 4 × 10⁵ N/m². The temperature is increased till it expands to triple its initial volume. What is the work done?

Solution:

Given: V_i = 2m³                 p = 4 × 10⁵ N/m²               V_f = 3V_i

The work done is

W = p(V_f – V_i) = p(3V_i – V_i)

     = (4 × 10⁵ N/m²)(6m³ – 2m³)

     = (4 × 10⁵ N/m²) × 4m³

     = 16 × 10⁵ J or 1.6 × 10⁶ J

Problem 2: A gas is kept in a container at 0.5 atm of constant pressure. It is compressed to half its initial volume of 200L. Calculate the work done and justify the sign convention.

Solution:

Given: p = 0.5 atm           V_i = 100L              V_f = ½ V_i

The work done is

W = p(V_f – V_i) = p( ½ V_i – V_i)

     = 0.5 atm × (100L – 200L)

     = (0.5 × 101325 N/m²)(-100 × 10^-3 m³)

     = 50662.5 N/m² × (-) 0.1 m³

     = -5066.25 J or -5.06625 kJ

Here, compression occurs, so ΔV is negative. Therefore, the net work done will also be negative.