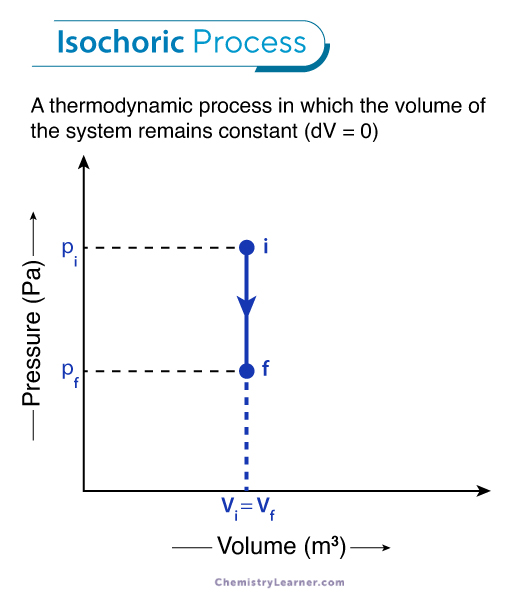
An isochoric process is a thermodynamic process occurring at a constant volume. It is also known as an isometric, isovolumetric, or constant-volume process. The term isochoric comes from the Greek words iso, meaning equal, and choric, meaning place or volume.

This process is reversible as the process is slow enough to retain internal equilibrium at every step.

Examples

Some examples of isochoric processes in daily life are:

• The ideal Otto cycle in internal combustion engines, in which the burning of the gasoline-air mixture increases the engine’s pressure and temperature while the volume remains unchanged.
• A gas stored in a sealed cylinder expands and contracts with temperature fluctuations keeping its volume constant.

Work Done In an Isochoric Process

The work done in a closed system is calculated by integrating the area under the p-V graph. A straight vertical line on the diagram, called an isochor, represents an isochoric process. The area covered by it is 0, which means there is no work done by or on the system during the process.

Mathematically, this is derived as

W = ∫pdV

or W = or, W = p ΔV

or, W = p (V_f -V_i)

Where

V_i: initial volume of the gas

V_f: final volume of the gas

Since the volume remains unchanged, we get

ΔV = 0

Therefore, W = 0

In isochoric conditions, only heat transfer can occur, and there is no change in volume during expansion or contraction. Thus, there is no pressure-volume work done, and only the internal energy of the system changes.

Heat Transfer and Internal Energy in Isochoric Process

From the first law of thermodynamics, we get the relation between the internal energy of a system (ΔU), the heat transferred during the process (Q), and the work done (W). Thus, we have

ΔU = ΔQ – ΔW

Here, ΔW = p ΔV, known as boundary work. Putting this in the expression above,

ΔU = ΔQ – p ΔV

Since there is no work done on or by the system, based on the first law of thermodynamics

∆U = ∆Q

The expression for enthalpy change is given as

H = U + pV

As ΔV = 0, the expression becomes

ΔH = ΔU = ΔQ

Hence, all the heat transferred to or from the system contributes to a change in internal energy. Based on the ideal gas model, the internal energy is:

ΔU = TΔS = m c_v ΔT

Where,

C_v: specific heat capacity at constant volume

m: mass of the gas

ΔT: change in temperature

ΔS:  change in entropy

Since the change in internal energy occurs solely due to heat transfer, we can state that for ΔU > 0, ΔT > 0. Using this relation in the ideal gas law, we get

ΔP = (nR/V)ΔT

Where

n: number of moles of the gas

R: gas constant

Putting (nR/V) as a constant, we derive a relation between the pressure and temperature in an isochoric process as

p_i/p_f = T_i/T_f

Thus, an increase in the temperature accompanies an increase in the gas pressure at constant volume in a closed system.

Substituting this relation in the equation for heat transfer derived from entropy, we have

ΔQ = mc_vT_i(p_f/p_i – 1)

Where

T_i: initial temperature of the gas

P_i: initial pressure of the gas

P_f: final pressure of the gas

Example Problems

Problem 1: In a sealed container, 0.1 moles of monoatomic gas are kept at 27°C. The container is then heated to 500K. Evaluate the work done and the change in the internal energy of the gas. (R = 8.315 J/mol.K)

Solution:

Given: n = 0.1 mol           T_i = 27°C + 273 = 300K          T_f = 500K       R = 8.315 J/mol.K           

For an isochoric process, ΔV = 0. Therefore there is no work done. From the first law of thermodynamics, we then get

ΔU = ΔQ

For a monoatomic gas, internal energy will thus be

ΔU = 3/2nRΔT = 3/2nR(T_f – T_i)

      = 3/2 (0.1 mol)(8.315 J/mol.K)(500K – 300K)

      = 3/2 (0.1 mol)( 8.315 J/mol.K)(200K)

ΔU = 249.45 J

Problem 2: 2 kg of water is heated from 50°C to 80°C in a closed vessel. What will be the change in the internal energy of the water? (specific heat of water = 4184 J/kg.K)

Solution:

Given: mass of water = 2 kg         T_i = 50°C = 323K                T_f = 80°C = 353K               c_v = 4184 J/kg.K

In an isochoric process, work done is 0. Hence the internal energy is only dependent on the heat absorbed. Thus,

ΔU = ΔQ = mc_vΔT

      = 2 kg × 4184 J/kg.K × (353K – 323K)

      = 2 kg × 4184 J/kg.K × 30K

ΔU = 251.04 kJ