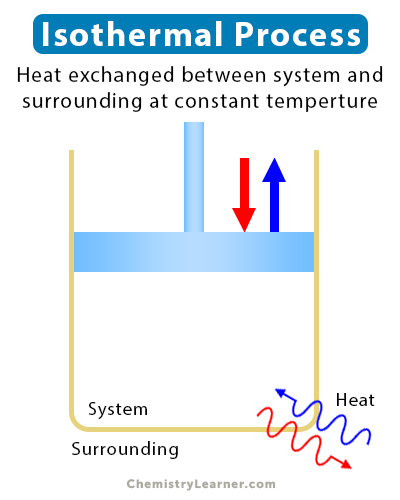
An isothermal process is a thermodynamic process whose temperature remains constant. During an isothermal process, a system exchange heat with its surroundings. The rate at which heat is exchanged is so slow that the system attains thermal equilibrium at every step. In some processes, the system exchanges heat with a reservoir, thus maintaining a thermal equilibrium at the latter’s temperature ^[1-4].

Examples ^[1]

• Phase transformation occurs at constant temperatures, such as melting, sublimation, and boiling.
• Some parts of the Carnot engine are carried out isothermally.
• A refrigerator dumps heat into the surroundings while maintaining a constant temperature.
• A thermostat keeps a house at a constant temperature by dumping heat outside during summer and bringing heat from outside in winter.

Isothermal Process and Boyle’s Law

Boyle’s law is a gas law establishing a relationship between pressure and volume for an isothermal process. According to this law, the pressure and volume are inversely proportional, provided the temperature and mass remain constant ^[3].

The following equation represents Boyle’s law:

P_iV_i = P_fV_f

Where

P_i: Initial pressure of the gas

V_i: Initial volume of the gas

P_f: Final pressure of the gas

V_f: Final volume of the gas

We will use this relationship later to calculate the work done.

Isothermal Process and First Law of Thermodynamics

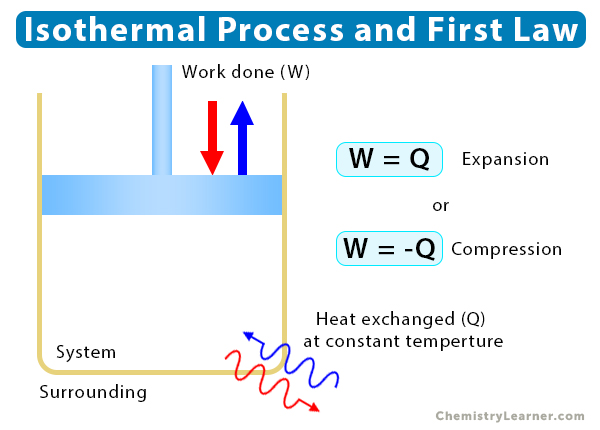
The first law of thermodynamics establishes a relationship between the internal energy (ΔU) of a system, heat transfer (Q), and work done (W). Mathematically, the first law is given by

ΔU = Q – W

Since internal energy is a function of temperature, its change for an isothermal process is zero, or ΔU = 0. Therefore,

 0 = Q – W

=> W = Q

It means that heat must be added for the system to do work. The amount of work done by the system equals the heat added to it when there is no change in temperature.

If heat is extracted from the system, then the expression for work done is

W = -Q

Let us calculate the reversible work done when an ideal gas is compressed or expanded isothermally.

Work Done in an Isothermal Process

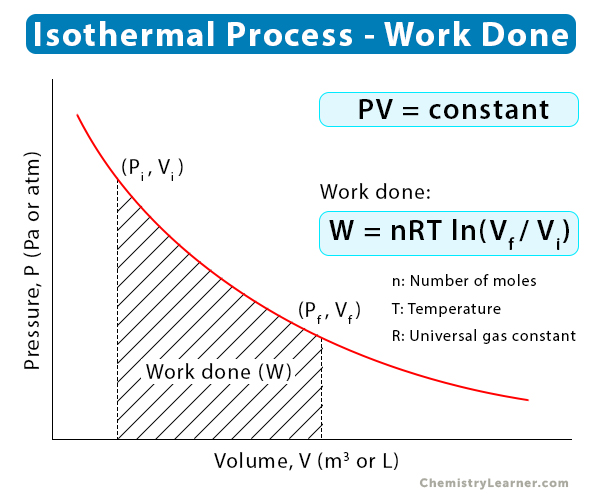
To calculate the work done for such a process, one must know how pressure (P) varies with volume (V) when the gas goes from its initial (i) to final (f) state. The P-V curve below shows that the pressure is inversely proportional to the volume. We take an infinitesimal area underneath the P-V curve and integrate it to get the work ^[2-5].

W = -∫PdV

According to ideal gas law

PV = nRT

=> P = nRT/V

Therefore

W = nRT∫dV/V

=> W = nRT ln (V_f/V_i)

Where

n: Number of moles of the gas

R: Universal gas constant

Sign Convention

If V_f > V_i, W > 0. It means that the gas expands and the work done is positive. If V_f < V_i, W < 0. It means that the gas compresses and the work done is negative. By convention, a positive value for work means the system does work on its surroundings. A negative value indicates that work is done on the system by the surroundings.

Example Problems

Problem 1: Three moles of a monatomic gas at a temperature of 27 ^oC expand isothermally from an initial volume of 20.0 m³ to a new volume of 40.0 m³. What is the work done by the gas?

Solution

Given

v_i = 20 m³            v_i = 40 m³            T = 27 ^oC = 273 + 27 = 300 K         n = 3      R = 8.314 J/mol·K

The work done is

W = nRT ln (V_f/V_i)

=> W = 3 mol x 8.314 J/mol·K x 300 K x ln (40 m³/ 20 m³)

=> W = 5186 J or 5.186 kJ

Problem 2: A balloon contains four moles of a diatomic gas. It is kept at a constant temperature of 25 ^oC. The balloon contracts to 30% of its initial volume. Find the work done on the gas in contracting the balloon.

Solution

Given

v_f/v_i = 30%          T = 25 ^oC = 273 + 25 = 298 K         n = 4      R = 8.314 J/mol·K

The work done is

W = nRT ln (V_f/V_i)

=> W = 4 mol x 8.314 J/mol·K x 298 K x ln (0.3)

=> W = -11932 J or – 11.932 kJ