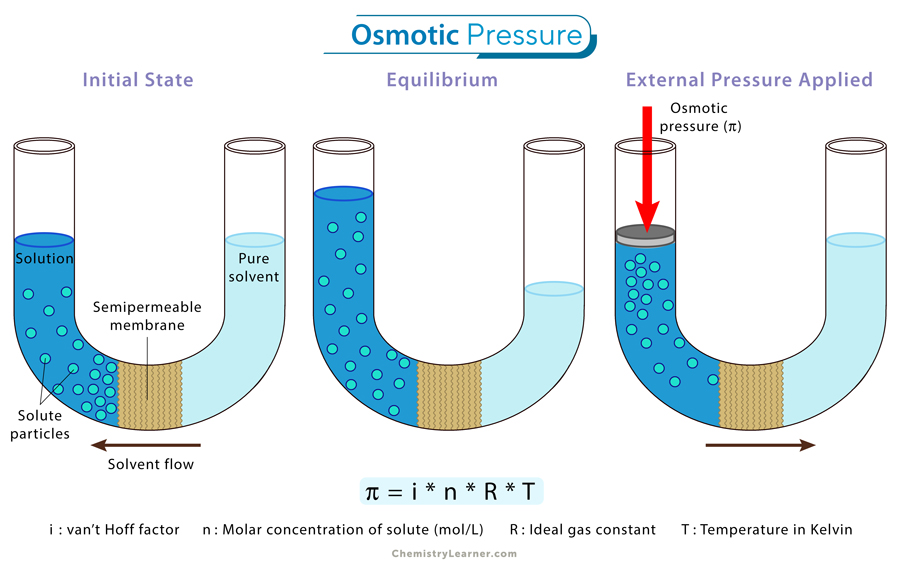
Osmotic pressure is the pressure a solvent exerts to prevent the inward flow of solvent molecules across a semipermeable membrane due to a difference in solute concentration on either side of the membrane. When there is a concentration gradient of solute across the membrane, solvent molecules move from a region of low solute concentration to a region of high solute concentration, which results in the establishment of osmotic pressure. ^[1-4]

Formula

The osmotic pressure is represented by the Greek letter π and is calculated using the following formula: ^[1-4]

π = i * M * R * T

Where

i: van’t Hoff factor

M: molarity of the solution, i.e., the number of moles of the solute per liter of the solution (mol/L)

R: ideal gas constant

T: absolute temperature (K)

Units and Dimension

Osmotic pressure is measured in units of atmosphere or atm. Other units include Pascal or Pa, pounds per inch or psi, and torr. The dimensional formula is [M¹L^-1T^-2].

It is essential to note that this formula applies to ideal solutions, where the solute particles do not interact with each other and do not undergo any chemical reactions.

Examples of Osmotic Pressure ^[1-4]

Plants

Plants rely on osmotic pressure to sustain their upright form. A well-hydrated plant absorbs water and expands its cells, which contain various salts. This cellular expansion increases pressure on the cell walls, enabling the plant to maintain its upright posture. In contrast, when the plant lacks an adequate water supply, its cells become hypertonic and shrink as water is lost. Consequently, the plant wilts and loses its sturdy, upright stance.

Blood Colloid

In the context of the circulatory system, osmotic pressure is essential for maintaining the balance of fluids between blood and tissues. The blood contains proteins, such as albumin, which are too large to pass through the blood vessel walls. These proteins create a high solute concentration in the blood, leading to significant osmotic pressure. This osmotic pressure draws water back into the blood vessels from the surrounding tissues, preventing excessive fluid loss and edema.

Desalination

Reverse osmosis utilizes osmotic pressure to achieve desalination, employing a higher pressure than the osmotic pressure to drive the movement of water across a semipermeable membrane while leaving the salt behind.

Hydrostatic Pressure vs. Osmotic Pressure

Hydrostatic pressure and osmotic pressure are two different forces that affect fluid movement. While osmotic pressure represents the pressure required to prevent solvent from flowing into a solution through a semipermeable membrane, hydrostatic pressure is the pressure exerted by water at rest or when it is not flowing in a confined space. This pressure is caused by the force of gravity. Therefore, the factors that affect hydrostatic pressure are density, depth of the water column, and acceleration due to gravity. For instance, the greater the water density or deeper the water column, the higher the hydrostatic pressure. ^[5]

Example Problems

Problem 1. A solution contains 0.2 moles of glucose dissolved in 1 liter of water. Calculate the osmotic pressure of the solution at 25 °C. (R = 0.0821 Lˑatm/molˑK).

Solution:

Given: n = 0.2 moles, V = 1 liter, R = 0.0821 Lˑatm/molˑK, T = 25 °C = 25 + 273 = 298 K

Since glucose does not disassociate, its van’t Hoff factor is 1.

The osmotic pressure is given by

π = i x M x R x T

=> π = 1 x (0.2 mol/ 1 L) x (0.0821 Lˑatm/molˑK) x (298 K) 

=> π = 4.89 atm

So, the osmotic pressure of the solution at 25 °C is 4.89 atm.

Problem 2. Calculate the osmotic pressure of 4.5% solution of cane sugar (sucrose) at the temperature of 17° C. (M.W. of sucrose = 342.3 g/mol)

Solution:

Given: Concentration = 4.5%, T = 17 °C = 17 + 273 = 290 K, M.W. = 342.3 g/mol

The solution contains 4.5 g of sucrose in 100 mL solution.

M = 4.5% = 4.5 g/100 mL = (4.5 g/342.3 g/mol) x 1/(100 x 10^-3 L) = 0.131 mol/L 

Moreover, i = 1 for sucrose.

The osmotic pressure is given by

π = i x M x R x T

=> π = 1 x 0.131 mol/L x 0.0821 Lˑatm/molˑK x 290 K

=> π = 3.12 atm 

Problem 3. The osmotic pressure of a sodium chloride solution at 300 K is 60 atmospheres. What is the molar concentration of sodium chloride in this solution?

Solution:

Given: π = 60 atm, T = 300 K

The osmotic pressure equation is

π = i x M x R x T  

=> M = π/(iRT)

The value of the van’t Hoff factor (i) is 2 since NaCl dissociates into two ions. Therefore, the molarity of NaCl is

M = (60 atm)/(2 x 0.0821 Lˑatm/molˑK x 300 K)

=> M = 1.21 mol/L

Therefore, the molar concentration of sodium chloride in the solution is 1.21 mol/L.

Problem 4. How much glucose per liter should be used for an intravenous solution to match the 7.65 atm at 37 °C osmotic pressure of blood? (M.W. of glucose = 180 g/mol)

Solution:

Given: π = 7.65 atm, T = 37 °C = 37 + 273 = 310 K, M.W. = 180 g/mol

For glucose, i = 1

The molar concentration of glucose is

M = π/(iRT)

=> M = 7.65 atm/(1 x 0.0821 Lˑatm/molˑK x 310 K)

=> n = 0.3 mol/L = (0.3 mol x 180 g/mol)/L = 54.1 g/L

There should be 54.1 grams per liter of glucose for an intravenous solution to match the 7.65 atm at 37 °C osmotic pressure of blood.