There exists a pressure at which the vapor formed above a liquid is in dynamic equilibrium with the liquid at a particular temperature. It means that the rate at which the liquid evaporates equals the rate at which the vapor condenses back. This pressure is the vapor pressure and is independent of the mass of the dissolved solute ^[1-4].

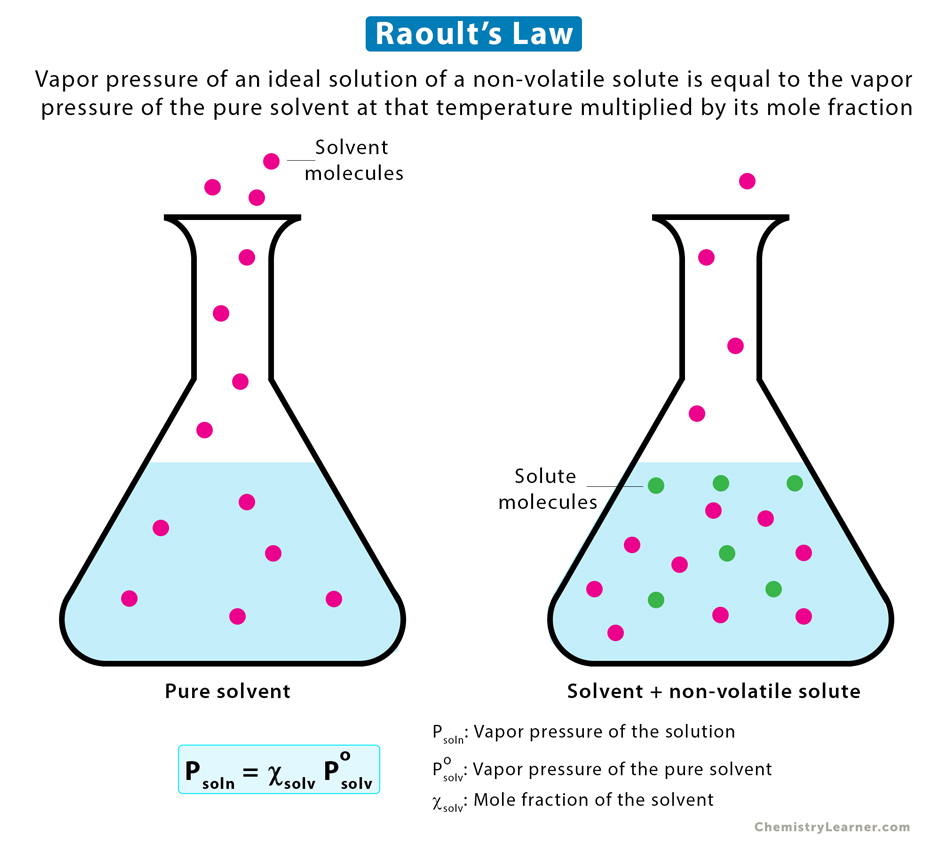
Raoult’s law states that “the vapor pressure of an ideal solution of a non-volatile solute is equal to the vapor pressure of the pure solvent at that temperature multiplied by its mole fraction.”

This law is named after French chemist François-Marie Raoult, who discovered it in 1887.

Equation

Raoult discovered that when a substance dissolves in a solvent, the solution’s vapor pressure (P_soln) depends on two factors^[1-4]:

1. The mole fraction of the amount of dissolved solute (χ_solv)
2. The original vapor pressure of the pure solvent (P^o_solv)

The following equation represents the above two observations:

P_soln = χ_solv * P^o_solv

The mole fraction of the solvent χ_solv is the fraction of the number of moles of the solvent present in the solution. Suppose n₁ moles of solutes mix with n₂ moles of a solvent. Then the mole fraction is

χ_solv = n₂ /(n₁ + n₂)

Explanation

Adding a solute to a solvent reduces the vapor pressure. It is because the added solute particles fill the gap between the solvent particles, thereby barring the latter from reaching the surface. It means that less number of solvent particles will be on the surface. This decreasing number reduces the chances of solvent particles escaping from the surface into the air above and entering the gas phase. However, the solvent particles in the vapor state can stick to the solute particles on the surface ^[1-3].

The result of all this is that there are fewer solvent particles in the vapor state at equilibrium, which lowers the saturated vapor pressure of the solution.

Raoult’s Law and Melting and Boiling Points

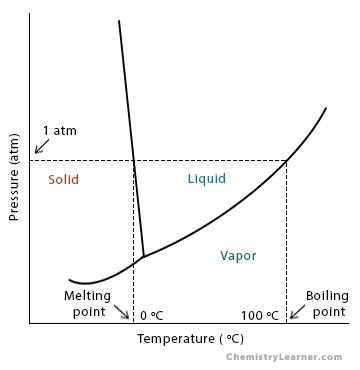
The fact that Raoult’s law affects the saturated vapor pressure of the solution enables us to study the melting and boiling points using phase diagrams. Let us take the example of water, whose phase diagram can be seen below. The standard boiling and melting points are shown in the diagram ^[1,2].

The curve separating the vapor and the liquid represents equilibrium. It can be considered as the effect of pressure on the boiling point. It can also be considered as the effect of temperature on the saturated vapor pressure. Therefore, there are two ways of looking at it. Notice that there is an equilibrium line for the solid-liquid interface. The triple point is where the liquid-vapor, solid-liquid, and solid-vapor curves meet. A horizontal line drawn on the phase diagram at 1 atm pressure gives the melting and boiling points of water. Now, let us look at the curve for a solution with a non-volatile solute.

The new equilibrium curves are shown in red in the above diagram. When a non-volatile solute is introduced, the liquid-vapor curve lowers and lies below the pure water curve. Consequently, this curve hits the solid-vapor curve at a point lower than that for pure water, thereby shifting the triple point. We draw a horizontal line at 1 atm pressure to determine the new melting and boiling points.

To summarize

• The boiling point of the solution is higher than the pure solvent. In other words, the boiling point rises.
• The melting point of the solution is lower than the pure solvent. In other words, the melting point decreases.

So far, we have discussed the effect of a non-volatile solute dissolved in water. However, this discussion extends to any solvent. The primary difference is in the solid-liquid equilibrium line. For water, this line slope backward. However, for most solvents, this line slope forward.

Limitations

Raoult’s law applies to ideal solutions. An ideal solution is one whose mixing characteristics are thermodynamically equivalent to an ideal gas, except that there is attraction among the molecules. It is not easy to obtain ideal solutions ^[1-3].

This law considers the number of moles of the solute that dissolves in the solvent. However, it does not consider the whether the solute will dissociate into its constituent ions. For example, when one mole of sodium chloride dissolves in water, it produces one mole of sodium ions and one mole of chloride ions. There is twice the number of ions as the original number of particles.

The law assumes that the intermolecular forces between solvent molecules are equal to those between solute and solvent molecules. It is not a valid point. As a result, deviations occur.

Deviations

Deviation from Raoult’s law occurs for certain liquids in a mixture. If adhesive forces between two such liquids exist, there will be deviations from Raoult’s law ^[1,2,4].

A negative deviation happens when the vapor pressure is lower than predicted by the law. It occurs when forces between particles are greater than those between particles in pure liquids. For example, this behavior occurs in a mixture of chloroform and acetone.

When the adhesive forces between similar molecules exceed that between dissimilar molecules, the resultant vapor pressure is higher than expected from the law. It is because both components of the mixture escape the solution more willingly than pure components. For example, this behavior occurs in a benzene and methanol mixture and a chloroform and ethanol mixture.

Example Problems

Problem 1: Consider a solution of ethanol at 25 ˚C. Suppose 25 grams of sucrose (342.3 g/mol) is added to 200 grams of ethanol (46.07 g/mol). The original vapor pressure for ethanol was 60 Pa. What is the new vapor pressure of the ethanol and sucrose solution at 25 ˚C?

Solution

Given m₁ = 25 g, m₂ = 200 g, P_solv^o = 60 Pa

The mole fraction of the solvent is given by

χ_solv = n₂ /(n₁ + n₂) = 200 g/(25 g + 200 g) = 0.89

The vapor pressure of the solution is given by

P_soln = χ_solv * P_solv^o = 0.89 x 60 Pa = 53.3 Pa

Problem 2: Suppose 2.0 moles of cherry Kool-Aid are added to a pitcher containing 1.5 liters of water at 25 ^oC. The vapor pressure of water alone is 22.4 mm Hg at 25 ^oC. What is the new vapor pressure of Kool-Aid?

Solution

Given n₁ = 2.0 mol, v₂ = 1.5 L, P_solv^o = 22.4 mm of Hg

1 L of water weighs 1000 g

1.5 L of water weigh = 1000 g/L x 1.5 L = 1500 g

18.02 g of water is equal to 1 mol

1500 g of water = 1 mol/ 18.02 g x 1500 g = 83.2 mol

The mole fraction of the solvent is given by

χ_solv = n₂ /(n₁ + n₂) = 83.2/(2.0 mol + 83.2 mol) = 0.977

The new vapor pressure of Kool-Aid is

P_soln = χ_solv * P_solv^o = 0.977 x 22.4 mm of Hg = 21.9 mm of Hg