The Van’t Hoff factor provides an understanding of how solutes impact the colligative properties of solutions. It refers to the ratio of moles of particles formed when a substance dissolves in a solution to the moles of formula units initially present. It is essential for electrolyte solution as it helps us understand the extent of ion dissociation in solution. Electrolytes break down into ions and carry an electric charge when dissolved in water. These ions are crucial in conducting electricity through the solution ^[1-4].

The van’t Hoff factor explains how many ions are produced when an electrolyte dissolves. For example, if a compound fully dissociates into two ions, the van’t Hoff factor is 2. However, some compounds may only partially dissociate, leading to a value between 1 and 2. When a non-electrolytic substance dissolves in water, the value is generally 1.

The van’t Hoff factor is named after Dutch chemist Jacobus Henricus van ’t Hoff, who pioneered his work on physical chemistry in the late 19^th century. 

Van’t Hoff Factor Formula

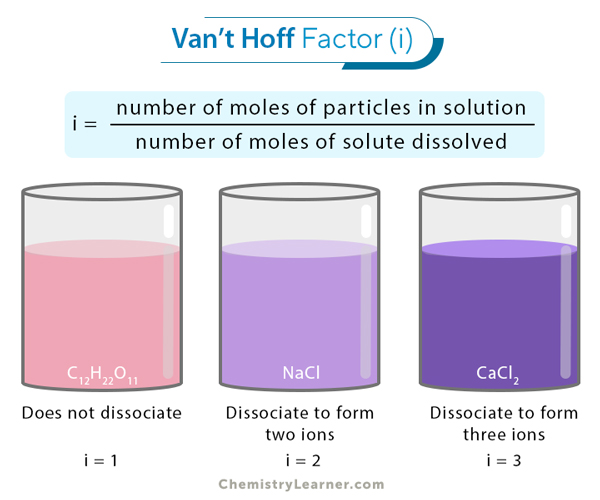
The van’t Hoff factor is denoted by the letter i. There are several ways of determining it. However, the most common way is to define it as the ratio of the number of moles of particles in solution to the number of moles of solute dissolved ^[1-8].

i = number of moles of particles in solution/number of moles of solute dissolved

Because solutes do not always fully dissociate in solution, another equation is often used.

i = 1 + α(n – 1)

Where, α is the fraction of solute particles dissociating in n number of ions.

The van’t Hoff Factor is a property of the solute. It does not depend on the concentration of the solution. It serves as an indicator of the departure from ideal behavior in a solution. A decrease in the van’t Hoff factor correlates with a more significant deviation.

Calculating van’t Hoff Factor

Calculating the van’t Hoff factor allows us to understand how solutes behave when they dissolve in a solvent ^[1-8]. 

Strong Electrolytes

For strong electrolytes, such as strong acids (HCl and HNO₃) or strong bases (NaOH and KOH), the van’t Hoff factor equals the total number of ions produced when the compound dissociates in water. For example, when NaCl dissolves in water, it fully dissociates into Na⁺ and Cl^– ions. Therefore, the van’t Hoff factor for NaCl is 2. Let us look at a few other examples.

CaCl₂ (s) → Ca²⁺ (aq.) + 2 Cl^– (aq.): i = 3

Fe₂(SO₄)₃ (s) → 2 Fe⁺ (aq.) + 3 SO₄^2- (aq.): i = 5 

Weak Electrolytes

Weak electrolytes, such as weak acids (acetic acid, CH₃COOH) or weak bases (ammonia, NH₃), partially dissociate into ions when dissolved in water. To calculate the van’t Hoff factor for weak electrolytes, we need to consider their degree of ionization or dissociation. It can be determined experimentally or estimated based on knowledge of the compound’s properties. For instance, acetic acid partially ionizes in water. If it is known that only 5% of acetic acid molecules dissociate into ions, the van’t Hoff factor would be 1.05.

Van’t Hoff Factor Table

The table below reveals that the measured values of the van’t Hoff factor for ionic compounds are slightly lower than expected, suggesting that their solutions contain fewer particles than predicted based on the number of ions per formula unit. However, some ions associate with each other in the solution, decreasing the total number of particles. The van’t Hoff factor decreases with increasing solute concentration because ionic compounds do not completely dissociate in aqueous solutions ^[1,2].

Compound	Measured Value	Ideal Value
Glucose	1.0	1.0
Sucrose	1.0	1.0
NaCl	1.9	2.0
HCl	1.9	2.0
MgCl2	2.7	3.0
FeCl3	3.4	4.0
Ca(NO3)2	2.5	3.0
AlCl3	3.2	4.0
MgSO4	1.4	2.0

Significance

The van’t Hoff factor is significant as it allows us to calculate various properties of electrolyte solutions, such as osmotic pressure, colligative properties like freezing point depression and boiling point elevation, and conductivity. Moreover, it helps predict electrolytes’ behavior in different conditions and concentrations, aiding in understanding the solubility of salts and their impact on chemical reactions ^[1].

References

1. Sciencenotes.org
2. Chem.libretexts.org
3. Mccord.cm.utexas.edu
4. Uochemists.com
5. Westfield.ma.edu
6. Saylordotorg.github.io
7. Jove.com
8. Dornshuld.chemistry.msstate.edu