We learned that the principal quantum number represents the distance of the electron from the nucleus of an atom, and hence, the atomic size. Let us study the following quantum number in the set.

What is Azimuthal Quantum Number

Also known as the angular momentum quantum number or orbital quantum number, the azimuthal quantum number determines the shape of the subshell in which the electrons reside. It is also used to calculate the orbital angular momentum of the electrons by applying the Bohr model. It is denoted by the symbol l and takes integer values ^[1-4].

Who Proposed Azimuthal Quantum Number

German physicist Arnold Somerfield proposed the azimuthal momentum quantum number based on his understanding of the Bohr model of the atom ^[1].

How to Determine the Azimuthal Quantum Number

The angular momentum quantum number can be found from the principal quantum number n. Once the value of n is known, the values of l range from 0 to n – 1. For example, when n = 4, the values of l are 0, 1, 2, and 3. The following table lists all the possible values of angular momentum quantum number ^[1-4].

Principal Quantum Number (n)	Azimuthal Quantum Numbers (l)
1	0
2	0,1
3	0,1,2
4	0,1,2,3
5	0,1,2,3,4
6	0,1,2,3,4,5
7	0,1,2,3,4,5,6

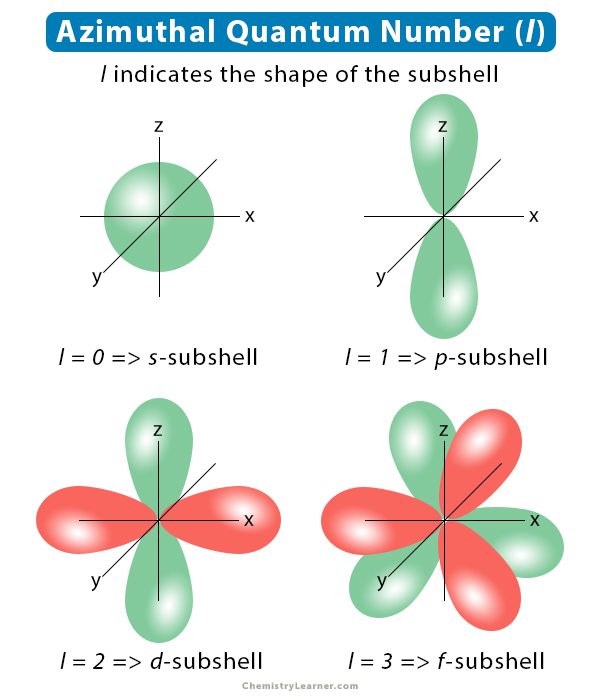
Azimuthal Quantum Number and Electron Subshell

The table below shows the first four azimuthal quantum numbers and their corresponding subshells ^[1-4].

Azimuthal quantum number (l)	Subshell
0	s
1	p
2	d
3	f

For example, when an electron resides in the 3p subshell, n = 3 and l = 1. Another example, n = 4, l = 2 represents the 4d subshell.

Consider the electron configuration of potassium: [Ar] 4s¹. According to this configuration, the valence electron resides in the 4s subshell.

Quantization of the Angular Momentum

Danish physicist Niels Bohr postulated that the angular momentum is quantized and its formula is given by ^[2],

L = sqrt √{l(l+1)} h/2π

Where,

L: quantized value of the angular momentum

l: azimuthal quantum number

h: Planck’s constant (= 6.626 x 10^-34 J.s)