Quantum Numbers
What are Quantum Numbers
Quantum numbers are a set of numbers used to define the state in which a fundamental particle like an atom, ion, nucleus, and electron resides. They represent the position, movement, and energy of the fundamental particle. For electrons, quantum numbers are significant since they designate the various discrete energy levels that the electrons can uniquely occupy [1-4].
How Many Quantum Numbers are There
There are four quantum numbers [1-4].
- Principal quantum number (n)
- Azimuthal quantum number (l)
- Magnetic quantum number (ml)
- Spin quantum number (ms)
1. Principal Quantum Number (n)
The principal quantum number describes the size of the electron shell of an atom. It takes positive integer values ranging from 1 to the shell number of the outermost electrons. The principal quantum number of an electron depends on the distance between it and the nucleus. The higher the number, the further the electron is. Therefore, it also represents the atomic and ionic radii.
How to Find the Principal Quantum Number
The principal quantum number of an element’s valence electron can be determined from the period in which the element resides in the periodic table. For example, potassium is in the fourth period and has a lone electron in its valence shell. Therefore, n = 4. Once the principal quantum number is found, the rest of the quantum numbers can be determined systematically.
Hydrogen and Hydrogen-like Atoms
A significance of the principal quantum number is that it can determine the electron energy for hydrogen and hydrogen-like atoms that have only one electron orbiting the nucleus. In the ground state, n = 1 and takes higher values in excited states. So, when the electron is excited, it absorbs energy and moves to a higher n-level. It has been found that the energy of the excited state is inversely proportional to the square of n.
2. Azimuthal Quantum Number (l)
The azimuthal quantum number, also known as angular momentum or orbital quantum number, describes the shape of the subshell in which the electron is present. It determines the magnitude of the electron’s angular momentum around the atom. Its values are whole numbers ranging from 0 to n – 1. For example, when n = 4, l = 0, 1, 2, 3. The various values of l represent the orbitals in which the electrons reside. These are indicated below.
- l = 0 implies s-orbital
- l = 1 implies p-orbital
- l = 2 implies d-orbital
- l = 3 implies f-orbital
The order of increasing energy of the orbitals is given by the Aufbau principle, which is useful to write the electron configuration of elements. For example, the electron configuration of oxygen is 1s22s22p4. Here, when n = 1, l = 0 indicates the s-orbital or 1s2. When n = 2, l = 0 indicates 2s2 and l = 1 indicates 2p4.
The azimuthal quantum number is significant since it indicates the atomic orbital shape and vibrantly affects chemical bonds and bond angles.
3. Magnetic Quantum Number (ml)
The magnetic quantum number describes the split in the electron’s energy sublevel into two or more levels. It is used to project the angular momentum along a specific axis. The number of splits is the total number of values that ml can take. This number is calculated from the l-value. The magnetic quantum number takes 2l+1 values ranging from -l to l. Each value represents an orbital.
For example, nitrogen has five electrons in its valence shell. Two are in the 2s-orbital and three are in the 2p-orbitals corresponding to l = 0 and l = 1, respectively. Therefore, the magnetic quantum number for l = 1 takes 2.1 + 1 = 3 values. These values and their corresponding orbitals are indicated as follows.
- ml = -1 represents py-orbital
- ml = 0 represents pz-orbital
- ml = +1 represents px-orbital
4. Spin Quantum Number (ms)
The spin quantum number represents the electron’s spin. It is used to project the spin angular momentum along a specific axis. For electron, it takes the values +1/2 and -1/2 depending upon the orientation of the spin, as indicated below.
- When ms = +1/2, the electron is in “spin-up” state
- When ms = -1/2, the electron is in “spin-down” state
According to Pauli exclusion principle, no two electrons can have the same four quantum numbers. When two electrons reside in the same orbital, their spins are opposite. It means they have the same n, l, and ml values. However, they differ in their ms value.
For example, magnesium has two valence electrons. It lies in the third period with a valency of two. Therefore, the two electrons reside in the 3s-orbital. Their quantum numbers are as follows.
- 1st electron: n = 3, l = 0, ml = 0, ms = +1/2
- 2nd electron: n = 3, l = 0, ml = 0, ms = -1/2
The image below shows all four quantum numbers and their representations.
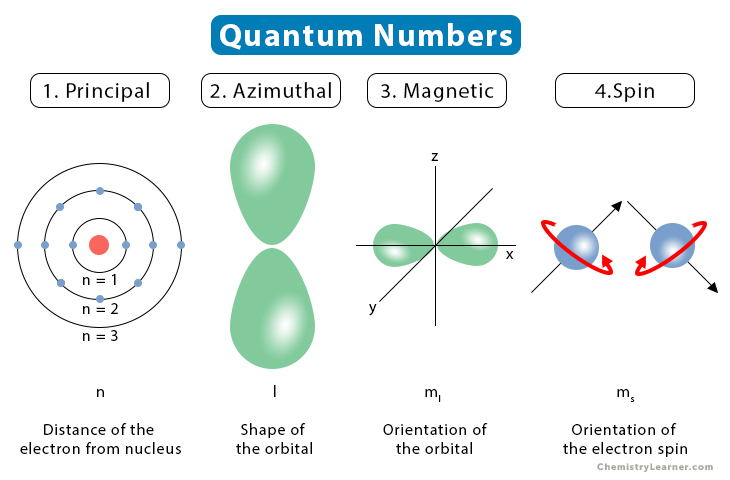
The following table summarizes all four quantum numbers, including the possible values that they can take [5].
| Quantum number | Symbol | Values | Signifies |
|---|---|---|---|
| Principal | n | 1, 2, 3, … | Distance from the nucleus |
| Azimuthal | l | 0, 1, 2, …, n-1 | Shape of the subshell |
| Magnetic | ml | -l, … , 0, … , +l | Orientation of the orbitals |
| Spin | ms | +1/2, -1/2 | Orientation of the electron spin |
The following chart shows the principal quantum number values ranging from 1 to 4, along with all the possible values that the corresponding azimuthal, magnetic, and spin quantum numbers can take.
| Principal quantum number (n) | Azimuthal quantum number (l) | Magnetic quantum number (ml) | Spin quantum number (ms) |
|---|---|---|---|
| 1 | 0 | 0 | +1/2, -1/2 |
| 2 | 0, 1 | -1, 0, 1 | +1/2, -1/2 |
| 3 | 0, 1, 2 | -2, -1, 0, 1, 2 | +1/2, -1/2 |
| 4 | 0, 1, 2, 3 | -3, -2, -1, 0, 1, 2, 3 | +1/2, -1/2 |
Problems and Solutions
Problem 1. What are the possible subshells when n = 3?
Solution: When n = 3, l = 0, 1, 2. Therefore, there are three possible subshells. They are 3s, 3p, and 3d.
Problem 2. How many orbitals are there in 4d-subshell?
Solution: The number of orbitals is given by 2l + 1.
d-subshell indicates l = 2. Therefore, there are 2 x 2 + 1 = 5 orbitals.
Problem 3. What are the possible values of ml for the d-subshell?
Solution. d-subshell correspondents to l = 2. Hence, the possible ml values are -2, -1, 0, +1, and +2.
Problem 4. Which orbital do the following quantum numbers represent: n = 4 and l = 3?
Solution. n = 4 and l = 3 represent the 4f-orbital.





Would be great to hear that voice explanation too.
Exceleent presentation of atomic structure which can be simply understandable by even primary students