Entropy is a thermodynamic state function that measures the randomness or disorder of a system. It is an extensive property, meaning entropy depends on the amount of matter. Since entropy measures disorder, a highly ordered system has low entropy, and a highly disordered one has high entropy. Entropy is often called the arrow of time because matter tends to move from order to disorder in isolated systems.

Entropy and the Second Law of Thermodynamics

A system at equilibrium does not undergo an entropy change because no net change is occurring. Generally, the combined entropy of the system and the surrounding for a spontaneous process increases. A positive entropy means an increase in disorder. These attributes of entropy are essential for formulating the Second Law of Thermodynamics.

How to Calculate Entropy

Entropy is a qualitative measure of how much the energy of atoms and molecules spreads during a process. It can be quantitatively measured in terms of a system’s statistical probabilities or other thermodynamic quantities.

Using Statistical Probability: Boltzmann Equation

The key assumption made here is that each possible outcome is equally probable, leading to the following equation:

S = k_B ln W

Where,

S: Entropy

W: Number of microstates corresponding to a given macrostate

k_B: Boltzmann’s constant (= 1.38 x 10^-23 JK^-1)

The above equation is known as Boltzmann Equation, named after Austrian physicist Ludwig Boltzmann. It is clear from this equation that entropy is an extensive property and depends on the number of molecules. When W becomes W², S becomes 2S. That is to say, doubling the number of molecules doubles the entropy.

Using Thermodynamic Quantities

Using statistical probability is very useful for visualizing how a process occurs. However, calculating probabilities like W can be very challenging. Entropy can also be derived from thermodynamic quantities that are convenient to measure.

Consider an ideal gas. For a reversible, isothermal expansion from volume V₁ to volume V₂ at temperature T, the heat absorbed by the gas is given by

Q_rev = nRTln(V₂/V₁)

Where n is the number of moles and R is the universal gas constant.

The change in entropy (ΔS) is the heat absorbed divided by the temperature.

ΔS = Q_rev /T = nRln(V₂/V₁)

Thus, the change in entropy depends upon the initial and final state of the system, indicating that it is a state function.

Symbol, Unit, and Dimension

The symbol for entropy is S, and in its standard state, it is S˚. The SI unit of entropy is J/K, and its dimension is [ML²T^-2K^-1].

Entropy Change Assessment

1. Temperature

According to kinetic theory, a substance’s temperature is proportional to the particles’ average kinetic energy. Increasing the temperature will impact the motion of the particles. It will result in rigorous vibrations in solids and rapid translations in liquids and gases. At higher temperatures, the kinetic energy distribution among the atoms or molecules becomes wider than at lower temperatures. Therefore, the entropy of any substance increases with temperature because more extensive molecular motion increases disorder.

2. Structure

Entropy is affected by the structure of the particles. The entropy is higher for substances made from heavy atoms than those from lighter ones. Molecules that are made up of more atoms, regardless of their masses, will have many ways to vibrate than molecules containing fewer atoms. Hence, these molecules have a higher W and entropy. Therefore, chemical reactions, where a substance changes from large and complex molecules to small and simple molecules, generally represent an increase in entropy.

3. Type of Particles

A substance may consist of one or more types of particles. Pure substances comprise one type of particle, meaning that all the particles are identical. On the other hand, mixtures comprise more than one type, meaning that there are nonidentical particles. In a mixture, the nonidentical particles have more orientations and interactions, increasing entropy.

For example, when a solid dissolves in a liquid, its molecules have greater freedom of movement and the ability to interact with the liquid molecules. It results in a more uniform dispersal of matter and energy, and the mixture will have more possible outcomes or value of W. Thus, the dissolution leads to an increase in entropy.

Example of Entropy

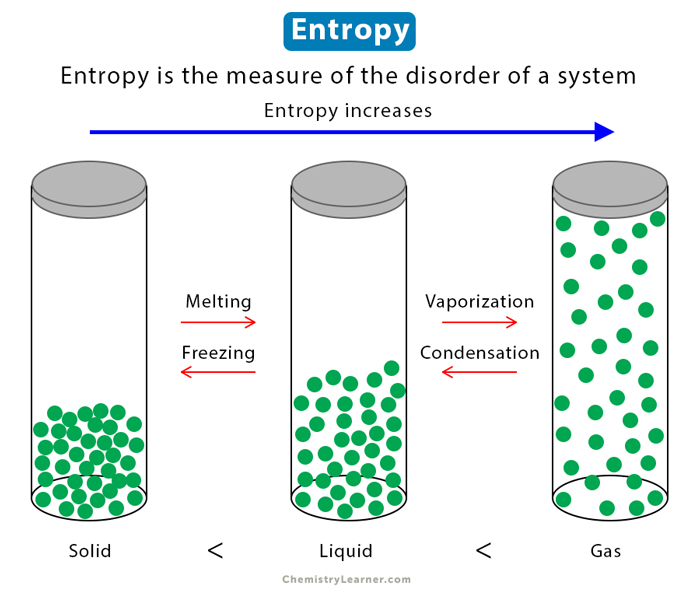
An example of entropy is the phase transfer that occurs when ice melts into water. Ice is a crystalline solid where molecules are fixed and arranged in a lattice. When ice melts into water, the molecules separate and move freely. However, they remain close to one another through hydrogen bonding. This increased freedom of movement leads to several possibilities for the molecules’ locations. As a result, W in the entropy equation increases, which increases entropy.

Now consider boiling water into water vapor. The molecules occupy more space than before, and each molecule can be found in more locations than ice and water. Therefore, the entropy in a gaseous state is the greatest for any substance, followed by the liquid state, and lowest in the solid state.

S_solid < S_liquid < S_gas

It also means that during melting, vaporization, and sublimation, entropy increases or ΔS > 0. On the other hand, during the reciprocal process, like condensation and freezing, entropy decreases or ΔS < 0.