The Gibbs free energy is the energy associated with a chemical process that can be used to do work. It is a state function that is defined in terms of three other state functions – enthalpy, temperature, and entropy. It is denoted by the symbol G. The formula for Gibbs free energy of a system is given by the enthalpy minus the product of the temperature and entropy ^[1-4].

G = H – TS

Where,

G: Gibbs free energy

H: Enthalpy

T: Temperature

S: Entropy

Unit: kJ/mol or kilo Joule per mole

American chemist J.W. Gibbs developed the free energy concept in the 1870s.

How to Calculate Gibbs Free Energy ^[1-5]

Change in Gibbs Free Energy

The change in Gibbs free energy is a useful term to determine the spontaneity of a thermodynamic process. It is defined as the difference between the Gibbs free energies of the final and the initial states of the system ^[2].

ΔG = G_final – G_initial

Consider a chemical reaction where reactants A and B combine to form products C and D. The equation is given by

A + B ⇌ C + D

Reactants ⇌ Products

Then, the change in Gibbs free energy is

ΔG = G_Products – G_Reactants

This change ΔG depends only on the initial and final values of the free energy and is independent of the path taken. It means that ΔG is independent of the reaction mechanism. From the equation for G, we get

ΔG = ΔH – Δ(TS)

This change is meaningful under two conditions – constant temperature and constant pressure. And, these conditions are typical in a laboratory. Therefore,

ΔG = ΔH – TΔS

Thus, the change in Gibbs free energy is equal to the change in enthalpy minus the product of temperature and change in entropy.

Determination of Spontaneity

The significance of the above equation is to determine the relative importance of the enthalpy and entropy terms as forces that drive a particular chemical reaction. This equation is used to determine the spontaneity of the reaction and predict in which direction it proceeds – forward or backward. Let us look at a few cases where the value of ΔG depends entirely on the values of ΔH and TΔS.

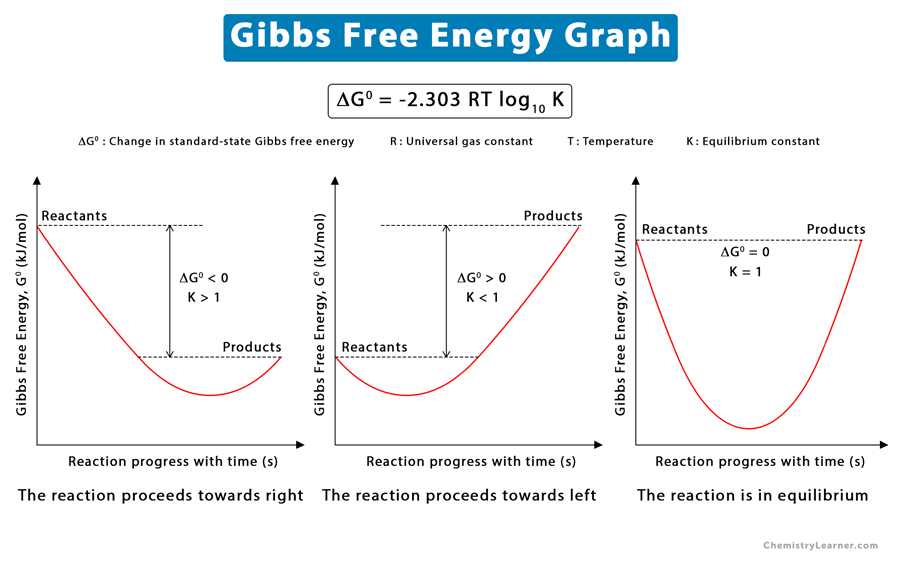
1. If ΔG < 0, the reaction is spontaneous and proceeds in the right or forward direction. It is known as spontaneous reaction or exergonic reaction.
2. If ΔG > 0, the reaction is nonspontaneous in the forward direction but spontaneous in the reverse direction. Hence, it will proceed toward the left. A nonspontaneous reaction is known as endergonic reaction.
3. ΔG = 0, the reaction is in equilibrium.

Standard-State Gibbs Free Energy

As mentioned before, the equation for ΔG applies to constant temperature and pressure conditions. When the reaction takes place at standard temperature and pressure (STP), the equation is rewritten as,

ΔG⁰ = ΔH⁰ – TΔS⁰

G⁰ is known as the standard-state Gibbs free energy, and ΔG⁰ is its change. This change can be calculated from the standard-state enthalpy and entropy tables.

National Institute of Standards and Technology (NIST) in Maryland, USA uses a temperature of 20 °C (293.15 K) and an absolute pressure of 1 atm (101.325 kPa) as the standard temperature and pressure. The difference between the change of standard-state Gibbs free energy ΔG⁰ and the change of Gibbs free energy ΔG is that the reactants and the products are at STP in the former.

Standard Gibbs Free Energy of Formation

The standard Gibbs free energy of formation of a substance is defined as the free energy change when 1 mole of the substance is prepared from its elements at standard temperature and pressure. It is denoted by ΔG_f⁰. The following table shows the standard Gibbs free energy of formation of a few substances.

Substance	Standard Gibbs Free energy of formation, ΔGf0 (kJ/mol.)
Water (liquid)	-237.14
Water (gas)	-228.61
Sodium chloride (solid)	-384.1
Ammonia (gas)	-16.4

Gibbs Free Energy at Equilibrium

Let us revisit the following chemical reaction.

A + B ⇌ C + D

As the reaction progresses, the Gibbs free energy changes with time. The change in Gibbs free energy can be expressed in terms of the change in standard-state Gibbs free energy.

ΔG = ΔG⁰ + RT ln Q

Where,

ΔG: Change in Gibbs free energy

ΔG⁰: Change in standard-state Gibbs free energy

R: Ideal gas constant (= 8.314 J/mol)

T: Temperature (in K)

Q: Reaction quotient (= [C][D]/[A][B])

Let us look at two different situations.

Case 1:

When Q = 1, ΔG = ΔG⁰

This point describes the standard-state conditions of the reaction, where ΔG is equal to the change in standard-state Gibbs free energy.

Case 2:

When ΔG = 0, Q = K

There is no driving force for the reaction, and the system is at equilibrium. Here, K is known as the equilibrium constant. Therefore,

0 = ΔG⁰ + RT ln K

Or, ΔG⁰ = – RT ln K

ΔG⁰ = -2.303 RT log₁₀ K

This equation gives the relationship between the standard-state Gibbs free energy and the equilibrium constant. It is used to determine the value of K from ΔG⁰ and vice versa.

Example of Gibbs Free Energy

Formation of Ammonia (NH₃)

Let us take the example of ammonia synthesis to understand Gibbs free energy further ^[3].

N₂ (g) + 3 H₂ (g) ⇌ 2 NH₃ (g)

The standard Gibbs free energy of formation of two moles of ammonia (NH₃) from nitrogen (N₂) and hydrogen (H₂) is ΔG_f⁰ = -32.8 kJ (see table above). This parameter is calculated when the reaction occurs at standard temperature and pressure. It means that the above reaction takes place at 293.15 K and 1 atm pressure.

The fact that ΔG_f⁰ is negative indicates that the reaction favors the formation of ammonia. In other words, under standard conditions, the reaction proceeds towards the right. The reactants are converted into products before reaching equilibrium. The magnitude of ΔG_f⁰ tells how far the standard-state is from equilibrium. The larger the value, the further the reaction from equilibrium.

Problems and Solutions

Problem 1. Calculate the ΔG for ice melting at 30 ˚C if the enthalpy and entropy of fusion of water are 6 kJ/mol and 22 J/mol-K.

Solution:

The reaction is,

H₂O (s) ⇌ H₂O (l)

Given,

ΔH_fus = 6 kJ/mol = 6000 J/mol

ΔS_fus = 22 J/mol-K

T = 30 ˚C = (273 + 30) K = 303 K

Gibbs free energy equation is given by

ΔG_fus = ΔH_fus – T ΔS_fus

Or, ΔG_fus = 6000 J/mol – 303 K x 22 J/mol-K

Or, ΔG_fus = -666 J/mol

The fact that ΔG_fus is negative indicates that the reaction is spontaneous in the forward direction. In other words, ice will melt into the water at 30 ˚C.

Problem 2. ∆G⁰ for the reaction below is 31.4 kJ/mol at 298.15 K. Use the thermodynamics parameters to decide in which direction the reaction is spontaneous when the concentrations of H₂SO₄ (aq.), HSO₄⁻ (aq.), and H₃O⁺ (aq.) are 0.5 M, 0.25 M, and 0.25 M respectively.

H₂SO₄ (aq.) + H₂O (aq.) ⇌ H₃O⁺ (aq.) + HSO₄⁻ (aq.)

Solution:

The reaction quotient is given by,

Q = [H₃O⁺ (aq.)][ HSO₄⁻ (aq.)]/[H₂SO₄ (aq.)]

    = 0.25 M x 0.25 M/0.5 M

    = 0.125

Given

ΔG⁰ = 31.4 kJ/mol = 31400 J/mol

T = 298.15 K

R = 8.314 J/mol-K

The change in Gibbs free energy is

ΔG = ΔG⁰ + RT ln Q

Or, ΔG = 31400 J/mol + 8.314 J/mol-K x 298.15 K x ln (0.125)

Or, ΔG = 26245 J/mol or 26.2 kJ.mol

Since ΔG > 0, the reaction is spontaneous in the reverse direction.