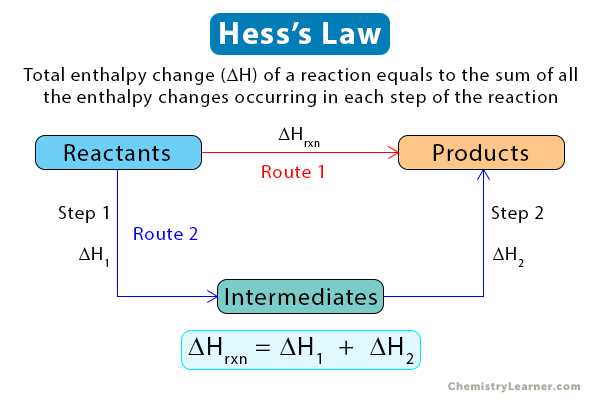
Hess’s law states that the total enthalpy change of a reaction equals the sum of all the enthalpy changes occurring in each step of the reaction. In other words, net enthalpy is independent of the number of steps the reaction takes to complete. Hess’s law is a consequence of the conservation of energy ^[1-4].

This law is essential because it establishes enthalpy as a state function. It allows us to calculate the overall enthalpy change by adding up the enthalpy changes for each step until the product is formed. For a reaction to obey Hess’s law, all the steps of the reaction must start and end at constant temperature and pressure.

This law is named after Russian chemist Germain Hess, who published it in 1840.

Equation

According to Hess’s law, enthalpy changes arising from the different steps are additive. Therefore, the overall enthalpy change of the reaction is the sum of all the enthalpy changes ^[1-5].

ΔH_rxn = ΣΔH_n

ΔH_rxn: Enthalpy change of the reaction

ΔH_n: Enthalpy change for each step

Examples ^[1-5]

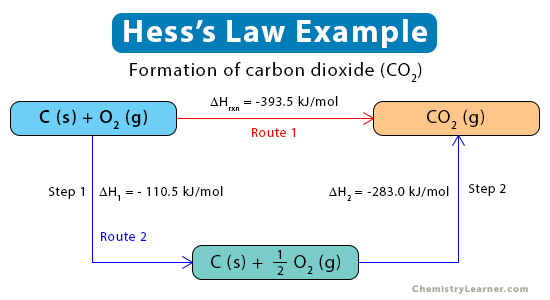
Example 1. Formation of carbon dioxide (CO₂) from graphite (C) and oxygen (O₂)

C (s, graphite) + O₂ (g) → CO₂ (g)

The above reaction occurs in two steps.

Step 1: Graphite reacts with oxygen to form carbon monoxide (CO) gas, releasing -110 kJ of energy per mole of CO.

C (s, graphite) + ½ O₂ (g) → CO(g)             ΔH = -110.5 kJ/mol

Step 2: Carbon monoxide reacts with oxygen forming carbon dioxide, releasing 283 kJ of energy per mole of CO₂.

CO (g) + ½ O₂ (g) → CO₂ (g)                          ΔH = -283.0 kJ/mol

Combining the two equations, we get the following equation:

C (s, graphite) + ½ O₂ (g) + CO (g) + ½ O₂ (g) → CO (g) + CO₂ (g)

Or, C (s, graphite) + O₂ (g) → CO₂ (g)

Which is the equation for formation of CO₂.

According to Hess’s law, we can combine the enthalpies to get the net enthalpy change or the enthalpy of formation of CO₂ gas.

ΔH_rxn= ΔH_f^o= -110.5 kJ/mol – 283.0 kJ/mol = -393.5 kJ/mol

The enthalpy change for the above reaction is represented in the diagram below.

Example 2. Formation of sulfur trioxide (SO₃) from sulfur (S) and oxygen (O₂).

S (s) + 3/2 O₂ (g) → SO₃ (g)

The above reaction occurs in two steps.

Step 1: Sulfur reacts with oxygen to form sulfur dioxide (SO₂), releasing 297 kJ of energy per mole of SO₂

S (s, graphite) + O₂ (g) → SO₂ (g)                               ΔH = – 297 kJ/mol

Step 2: Sulfur dioxide reacts with oxygen to produce sulfur trioxide and 98 KJ of energy per mole of SO₃

SO₂ (g) + ½ O₂ (g) → SO₃ (g)                         ΔH = -98 kJ/mol

Combining the two equations

S (s, graphite) + O₂ (g) + SO₂ (g) + ½ O₂ → SO₂ (g) + SO₃ (g)

Or, S (s) + 3/2 O₂ (g) → SO₃ (g)

Which is the equation for formation of SO₃ gas.

Using Hess’s law to combine the two enthalpy changes

ΔH_rxn= ΔH_f^o= -297 kJ/mol – 98 kJ/mol = -395 kJ/mol

Solved Problems

Problem 1: Find the net enthalpy change (∆H_rnx) of the reaction below.

CS₂ (l)  +  3 O₂ (g)  →  CO₂ (g)  +  2 SO₂ (g)

The reactions in each step and their corresponding enthalpy change are given below.

C (s) + O₂ (g) → CO₂ (g)                  ΔH = -393.5 kJ/mol                         (i)

S (s) + O₂ (g) → SO₂ (g)                   ΔH = -295 kJ/mol                             (ii)

C (s) + 2S (s) → CS₂ (l)                     ΔH = +90 kJ/mol                              (iii)

Solution

1. We leave reaction (i) as it is since CO₂ is a product in the primary reaction.

2. We multiply reaction (ii) by 2 since we want 2 moles of CO₂. The enthalpy change will also be multiplied by 2.

2 S (s) + 2 O₂ (g) → 2 SO₂ (g)                       ΔH = -590 kJ/mol                             (iv)

3. We flip reaction (iii) since we want CS₂ to be a reactant.

CS₂ (l) → C (s) + 2S (s)                     ΔH = -90 kJ/mol                (v)

Adding all the reactions together

C (s) + O₂ (g) + 2 S (s) + 2 O₂ (g)  + CS₂ (l) → CO₂ (g) + 2 SO₂ (g) + C (s) + 2 S (s)

Or, CS₂ (l)  +  3 O₂ (g)  →  CO₂ (g)  +  2 SO₂ (g)

Let us apply Hess’s law to calculate the net enthalpy.

ΔH_rxn = -393.5 kJ/mol + (-590 kJ/mol) + (-90 kJ/mol) = -1073.5 kJ/mol