Magnetic Quantum Number
We learned that the principal quantum number represents the energy of the electron shell, and the azimuthal quantum number represents the shape of the subshell. Let us study the third quantum number in the set.
What is Magnetic Quantum Number
The magnetic quantum number divides the subshell into orbitals and determines their number. Each value of the magnetic quantum number represents a specific orientation of the orbital having fixed energy and shape [1-4].
Who Introduced Magnetic Quantum Number
German-American physicist Alfred Landé proposed the magnetic quantum number to explain the Zeeman Effect.
How to Find Magnetic Quantum Number
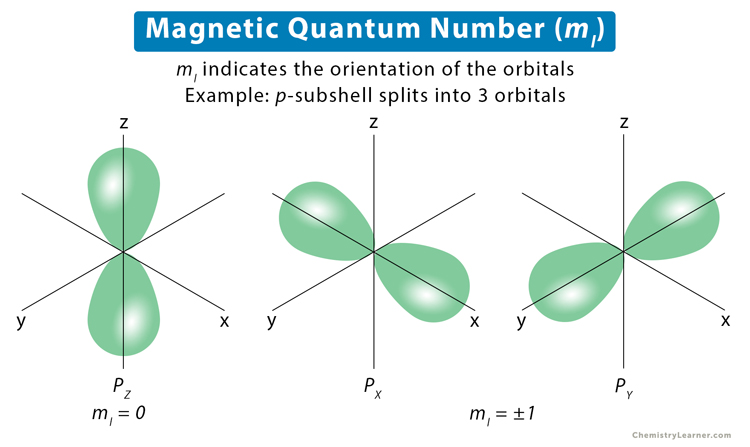
The magnetic quantum number is denoted by the symbol ml, whose values depend on the azimuthal quantum number l. The formula is as follows. For each value of l, ml takes values ranging from -l to +l. The total number of allowed values of ml is 2l + 1. For example, the l = 1 represents the p-subshell. The values of the magnetic quantum numbers are: ml = -1, 0, +1. Each value corresponds to a unique orientation of the p-subshell designated as px, py, and pz. Their orientations are shown in the image below [1-6].
Now, each subshell has an associated energy. The various energy levels of the subshells depend on n and l. The magnetic quantum number splits each energy level into 2l + 1 levels. For example, suppose an electron is found in the 3d sublevel. The magnetic quantum number splits the 3d sublevel into five energy levels such that the values of ml are-2, -1, 0, 1, and 2. The following table shows all the possible values of the ml.
| Azimuthal quantum number (l) and the corresponding subshell | Number of orbitals or orientations of the orbital (2l + 1) | Magnetic quantum number (ml) |
|---|---|---|
| 0 (s-subshell) | 1 | 0 |
| 1 (p-subshell) | 3 | -1, 0, 1 |
| 2 (d-subshell) | 5 | -2, -1, 0, 1, 2 |
| 3 (f-subshell) | 7 | -3, -2, -1, 0, 1, 2, 3 |