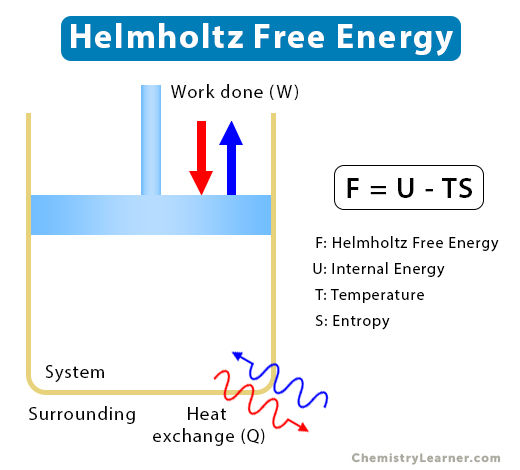
The Helmholtz free energy is a state function that characterizes the aspects of work. It measures the valuable work obtained from a closed thermodynamic system at a constant temperature. At constant temperature or isothermal process, the system exchanges heat with the surrounding, as shown in the image below. Either, work is done on the system and heat is released to the surrounding, or work is done by the system and heat is absorbed from the surrounding. Thus, Helmholtz free energy is a measure of the amount of energy that goes to create a system once the spontaneous energy transfer from the surrounding to the system is accounted for ^[1-4].

German physicist Hermann von Helmholtz first presented the free energy concept in 1882.

Helmholtz Free Energy Equation ^[1-6]

The Helmholtz free energy is written in terms of other thermodynamical variables. Mathematically, it is defined as the internal energy minus the product of temperature and entropy. It can be determined by using the following equation.

F = U – TS

Where,

F: Helmholtz free energy of the system

U: Internal energy of the system

T: Absolute temperature in Kelvin

S: Entropy of the system

Symbol: F

Unit: kJ/mol or kilo Joules per mole

To create a system that is in equilibrium with the surrounding with the above variables, energy must be provided. A part of the energy (U) can be obtained as heat from the surrounding. This heat (TS) is given by the product of temperature and entropy. The rest of the energy must be provided as work (F).

On the contrary, if the system is destroyed at constant temperature (T), the entropy must be reduced to zero by heat (TS) transfer to the surrounding. The remaining work (F) can be extracted for “free”. Hence, the energy is called free energy.

Therefore, the Helmholtz free energy can be thought of as the energy available to do work on a system at temperature T, with energy U, and with entropy S.

Change of Helmholtz Free Energy

The Helmholtz free energy is a powerful quantity for studying isothermal processes. A more practical approach to it is to study its change. At a constant temperature, the change in Helmholtz free energy is given by

ΔF = ΔU – TΔS

From the first law of thermodynamics, when work W is done on a system, it releases heat Q. The change in internal energy is given by

ΔU = Q + W

From the second law of thermodynamics, for a closed system undergoing a reversible process

Q = TΔS

Then, ΔF becomes

ΔF = Q + W – TΔS

Or, ΔF = W

For an irreversible process, the following inequality holds true for a closed system.

TΔS ≥ Q

Or, Q – TΔS ≤ 0

From the ΔF equation,

ΔF = W + (Q – TΔS)

Or, ΔF = W + a negative quantity

Or, ΔF ≤ W

Thus, the Helmholtz free energy is a measure of the work done in a reversible isothermal process. Free energy is available to do work at a constant temperature. Here, work is any kind of work and not just the compressional (PV) work. The change in Helmholtz free energy is maximum for a reversible isothermal process.

Suppose no work is done on the system, nor does the system does any work on the surrounding. Then, W = 0 implies ΔF ≤ 0. It means that when no work is done at a constant temperature, the system exchanges heat with the surrounding, and the Helmholtz free energy cannot increase. As the system moves towards equilibrium, F will decrease until it reaches a constant value at equilibrium. Thus, the equilibrium is the state of minimum Helmholtz free energy.

Gibbs vs. Helmholtz Free Energy ^[2]

The following table gives the difference between Gibbs free energy and Helmholtz free energy.

	Gibbs Free Energy	Helmholtz Free Energy
Definition	Maximum reversible work obtained from a system	Valuable work obtained from a closed system
Conditions	Constant temperature and pressure (isothermal and isobaric)	Constant temperature (isothermal)
Equation	G = H – TS	F = U – TS
Used	Often, since constant temperature and pressure conditions are widely used in laboratory and industry	Rarely
Application	To predict the spontaneity of a reaction	To study explosive reaction