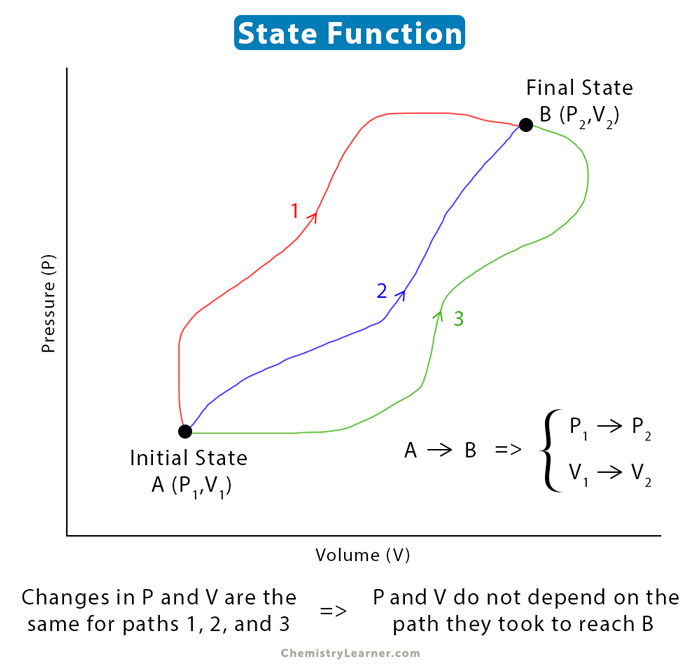
A state function is a thermodynamic quantity that depends only on the present state of a system and not on how the system arrived at that state. It describes the system’s equilibrium state. In contrast, a path function depends on how it arrived at the present state from a former state ^[1-4].

List of State Functions

• Pressure
• Temperature
• Volume
• Mass
• Internal Energy
• Gibbs Free Energy
• Entropy
• Enthalpy

Equation

Consider a state function φ whose initial value is φ₁ and the final value is φ₂. Then, the change in the state function is given by ^[1-7]

Δφ = φ₂ – φ₁

Thus, the change in state function is the difference between its final value and initial value.

Example

Suppose we have 1 M of helium gas that occupies a volume of 10 L at 300 K, which is the initial state. The gas is allowed to expand adiabatically to 20 L while its temperature changes to 500 K, which is the final state. Let us again go back to the initial state and allow the gas to expand isothermally at 300 K to 20 L. Note that the volume changed from 10 L to 20 L in both adiabatic and isothermal processes. Mathematically, this can be written as

ΔV = 20 L – 10 L = 10 L

Irrespective of how the gas expanded from its initial to the final value, the final volume is always 20 L. It implies that volume is a state function.

Integral Form

The change in state function can also be expressed in integral notation. To evaluate the integral, one needs to know three things – the function, the lower limit, and the upper limit. In other words, integral highlights that state function depends on the initial and final values. Based on this concept, let us look at the expression for enthalpy (H) change in integral form.

∫H(t)dt = H(t₂) – H(t₁)

This equation is similar to the enthalpy change that we are familiar with.

ΔH = H_final – H_initial

State Function and Path Function ^[1-7]

Similarities

• Both are thermodynamic quantities
• Both define the properties of a thermodynamic system

Difference

State Function	Path Function
A physical quantity with a specific value that does not depend on how it reached that value	A physical quantity with a specific value that depends on how it reached that value
Also known as a point function	Also known as a process function
Can be integrated easily using the knowledge of initial and final values	Requires several integrals and knowledge of limits for each integral
Its value remains the same regardless of the path taken to obtain that value	Its value will change if the path taken to reach that value is different for each process
Examples include internal energy, enthalpy, pressure, volume, and temperature	Examples include heat and work