The Nernst equation is used to calculate the electrochemical cell potential at any known pressure, temperature, and concentration. This equation relates the reduction potential of a cell at a non-standard condition to that at the standard conditions.^[1-4]

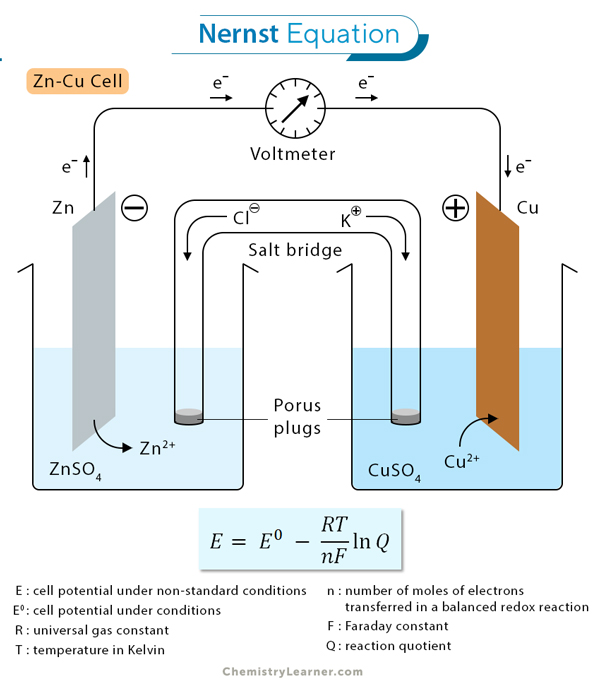
An electrochemical cell consists of two half-cells, each containing a different electrode immersed in an electrolyte solution. These half-cells are connected by a conductive pathway, allowing the movement of electrons between them. The Nernst equation helps us understand and predict the behavior of this electron transfer. It enables us to calculate the cell potential under non-standard conditions by considering the concentrations of reactants and products in each half-cell.

The equation is named after Walther Nernst, a German physical chemist who formulated it in 1887.

Expression

The Nernst equation is mathematically expressed as:^[1-8]

E = E° – (RT/nF) ln(Q)

Where

E is the cell potential under non-standard conditions.

E° is the standard cell potential under standard conditions.

R is the ideal gas constant.

T is the temperature in Kelvin.

n is the number of moles of electrons transferred in a balanced redox reaction.

F is the Faraday constant.

Q is the reaction quotient, the ratio of product and reactant concentrations at non-standard conditions.

The unit of the electrochemical potential is Volts or V. To find n, the most effective approach is to write the half-reactions for oxidation and reduction and subsequently balance the equations to ensure an equal number of electrons in both.

Derivation

The Nernst equation derivation comes from the Gibbs free energy equation. The change in Gibbs free energy (ΔG) is related to the potential difference (E) under general conditions (standard or not).^[1,4,5]

ΔG = -nFE

Under standard conditions, the equation becomes 

ΔG° = -nFE°

A positive E° indicates a spontaneous reaction, while a negative E° indicates a non-spontaneous reaction.

The Gibbs energy change under non-standard conditions can be related to the standard Gibbs energy change.

ΔG = ΔG° + RT ln(Q)

Substituting ΔG = -nFE and ΔG° = -nFE° into equation, we obtain

-nFE = -nFE° + RT ln(Q)

Dividing both sides by -nF gives us the Nernst equation.

E = E° – (RT/nF) ln(Q)

The Nernst equation can be simplified further. At standard temperature, T = 298 K. Also, R = 8.314 JˑM^-1ˑK^-1 and F = 96485 CˑM^-1. Therefore,

E = E° – ((8.314 JˑM^-1ˑK^-1 x 298 K)/(n x 96485 CˑM^-1) ln(Q)

=> E = E° – (0.0257 V/n) ln(Q)

=> E = E° – (0.0257 V/n) x 2.303 log(Q)

=> E = E° – 0.0591 V/n log(Q)

Applications

The Nernst equation finds applications across various scientific fields. Some notable applications include:^[3]

• Batteries and Fuel Cells: It plays a fundamental role in understanding battery performance and fuel cell behavior, guiding the design and optimization of these energy storage and conversion devices.
• Corrosion Studies: It aids in assessing the corrosion rate of metals and helps design effective corrosion protection strategies.
• pH Measurements: It is involved in determining the pH of a solution using pH electrodes, contributing to accurate acidity and alkalinity measurements in various fields, including environmental monitoring and medical diagnostics.
• Analytical Chemistry: It is applied in electroanalytical techniques like potentiometric titrations, enabling the quantitative determination of various analytes in solution.

Nernst Equation and pH

The Nernst equation determines the cell potential of reactions that depend on pH. If H⁺ is involved in the cell reaction, the electrochemical potential will depend on the pH. Consider the following half-reaction:^[1]

½ H₂ → H⁺ + e⁻

The reaction quotient is

Q = [Product]/[Reactant] = [H⁺]/[H₂]^1/2

Since there is only one hydrogen atom present, [H₂]^1/2 = 1

Therefore, 

Q = [H⁺]

Hydrogen’s standard electrode potential (E°) is taken to be zero volts at all temperatures, that is, E° = 0.

We use the simplified Nernst equation

E = E° – 0.0591 V/n log(Q)

=> E = E° – 0.0591 V/1 log [H⁺]

Since n =1 and pH = – log[H⁺], we get

E = 0.591 x pH

Example Problems

Problem 1. Consider a galvanic cell with a copper electrode in a 0.1 M Cu²⁺ solution and a silver electrode in a 0.01 M Ag⁺ solution. The standard reduction potentials for Cu²⁺ and Ag⁺ are +0.34 V and +0.80 V, respectively. Calculate the cell potential at 25°C.

Solution:

The Nernst equation is given by

E = E° – (RT/nF) ln(Q)

The balanced half-reactions are

Reduction: Cu²⁺ + 2e- → Cu

Oxidation: 2 Ag → 2 Ag⁺ + 2e-

The cell reaction is the sum of these two half-reactions.

Cu²⁺ + 2 Ag → Cu + 2 Ag⁺

Given 

[Cu²⁺] = 0.1 M, [Ag⁺] = 0.01 M, E°_reduction = +0.34 V, E°_oxidation = +0.80 V, n = 2, T = 298 K

The cell potential for the given galvanic cell is

E_cell = E°(reduction) – E°(oxidation) = +0.34 V – (+0.80 V) = -0.46 V

The reaction quotient Q is

Q = [Cu][Ag⁺]²/[Cu²⁺][Ag]²

The concentrations of copper and silver are taken to be 1 in standard conditions, that is, [Cu] = [Ag] = 1. Therefore,

Q = (1 M x (0.01 M)²)/( 0.1 M x 1 M) = 0.001

The Nernst equation simplifies to

E = -0.46 V – (((8.314 JˑM^-1ˑK^-1 x 298 K)/(2 x 96485 CˑM^-1) ln(0.001) = – 0.371 V

The cell potential at 25°C is approximately -0.371 volts. Since this value is negative, the cell reaction is non-spontaneous under these conditions.