Formal Charge
What is a Formal Charge [1-8]
A formal charge is a charge assigned to an atom in a molecule, assuming that all electrons in the chemical bonds are shared equally between the atoms. This assumption excludes the electronegativity difference between the atoms. The sum of formal charges of all the atoms is equal to the compound’s actual charge. If the compound is neutral, the net formal charge is zero.
How to Calculate the Formal Charge [1-7]
In order to calculate the formal charge of a molecule or an ion, one has to know about Lewis structure and resonance. A Lewis dot structure is a straightforward representation of valence shell electrons in an atom, ion, or molecule. It shows how electrons are positioned around the atoms of the compound. Dots represent paired electrons, and dash lines show bonded electrons.
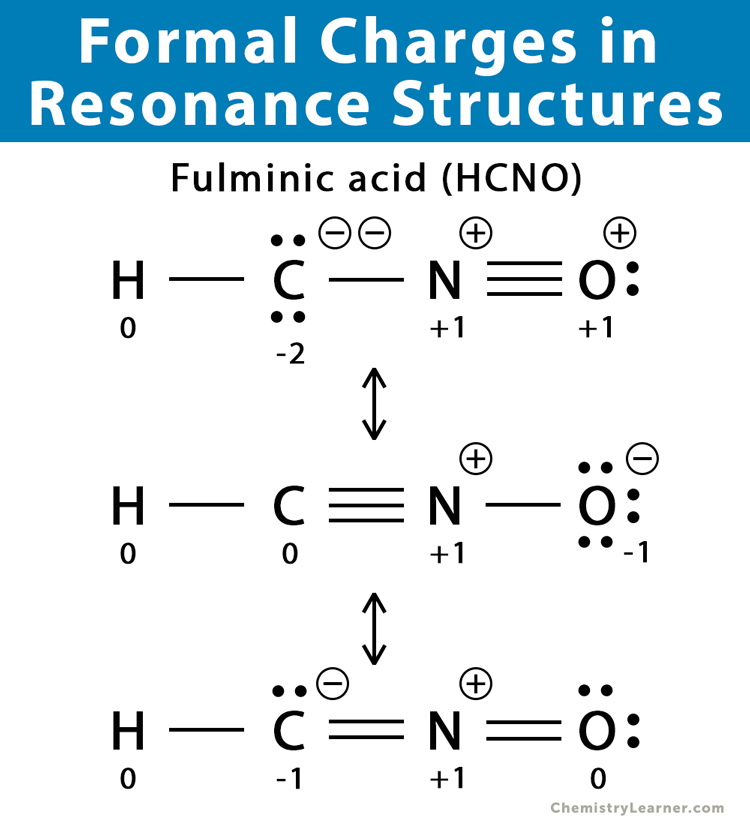
Sometimes more than one Lewis structure can be drawn to represent the same compound. The difference among these structures is the position of the electrons and bond formation. The free electrons can move throughout the compound and are said to be delocalized. This phenomenon of shifting electrons among the atoms is known as resonance. These equivalent structures are known as resonance structures. Depending on the compound, the shifting of electrons may cause a change in the atoms’ formal charges. However, the net formal charge in all the resonance structures remains the same.
From the Lewis structure representation of the compound, the formal charge can be calculated by two methods.
1. Using Equation
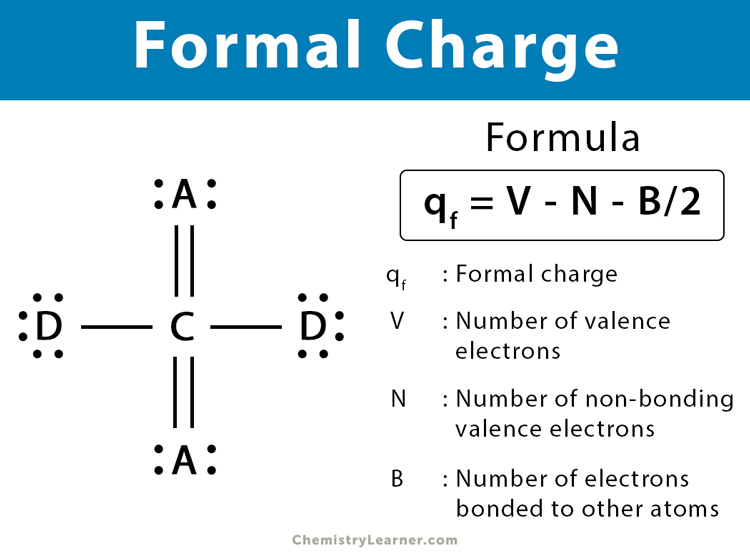
The following formula gives the formal charge of an atom in a molecule.
qf = V – N – B/2
where,
V: number of valence electrons of the neutral atom
N: number of non-bonding valence electrons of the neutral atom (also known as lone pair electrons)
B: total number of electrons shared in bonds with other atoms
This formula explicitly gives the relationship between the number of bonding and non-bonding electrons. It states how many electrons are formally “owned” by the atom. The number of valence electrons for an atom is equal to its group number.
Examples
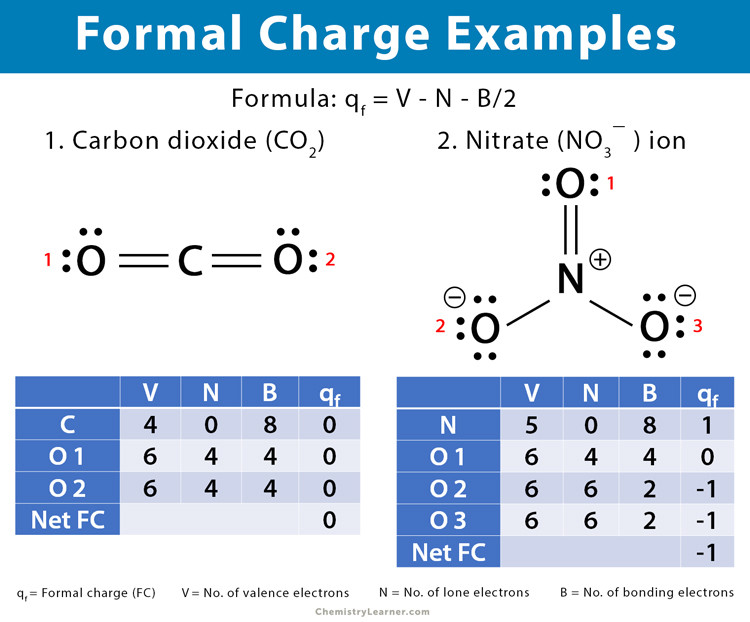
1. Carbon dioxide (CO2)
Carbon (C) has a double bond with each of the oxygen (O) atoms. The structure of CO2 is O=C=O.
For carbon,
V = 4, N = 0, B = 8
Therefore, formal charge on carbon in CO2 is given by,
qf = 4 – 0 – 8/2 = 0
For oxygen,
V = 6, N = 4, B = 4
Therefore, formal charge on oxygen in CO2 is given by,
qf = 6 – 4 – 4/2 = 0
The net formal charge is,
0 + 0 + 0 = 0
Thus, the formal charge of CO2 is zero.
2. Nitrate (NO3–)
Nitrogen (N) has a double bond with one oxygen (O) atom and two single bonds with two other oxygen atoms. The three bonds in NO3– are represented by O=N+, N+-O–, and N+-O–.
For nitrogen,
V = 5, N = 0, B = 8
Therefore,
qf = 5 – 0 – 8/2 = 1
The formal charge on nitrogen in NO3– is 1
For oxygen 1,
V = 6, N = 4, B = 4
Therefore,
qf = 6 – 4 – 4/2 = 0
For oxygen 2 and oxygen 3,
V = 6, N = 6, B = 2
Therefore,
qf = 6 – 6 – 2/2 = -1
The net formal charge is,
1 – 0 – 1 – 1 = – 1
Thus, the formal charge of NO3– is -1.
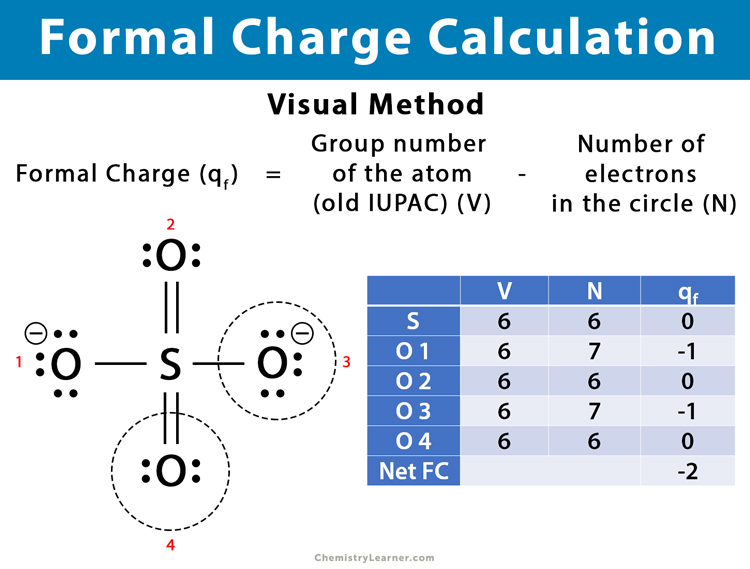
2. Visual Method
Apart from the formula, the formal charge can be calculated pictorially using the diagrammatic method. Here are the steps to calculate the formal charge.
Step 1: Draw a circle around the atom for which the formal charge is being calculated
Step 2: Count the number of electrons in the concerned atom’s circle, including electrons shared in covalent bonds.
Step 3: The formal charge is given by,
Formal charge = group number (old IUPAC) of the atom – electrons in the atom’s circle
Below is an example of calculating the formal charge of SO42- using the visual method.
Formal Charges of Some Common Compounds
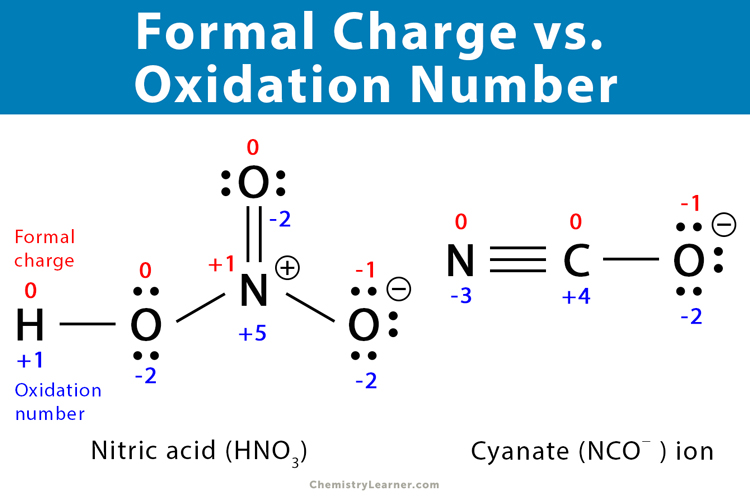
Oxidation Number vs. Formal Charge [8]
The oxidation number is the number of electrons a particular atom can lose, gain, or share with another atom. This term applies to any atom in a molecule. However, it is commonly used for the central metal atoms of coordination complexes. The oxidation number gives the degree of oxidation of an atom in a compound and is a whole number.
The critical difference between formal charge and oxidation number is that the formal charge is the charge of an atom in a molecule that is calculated assuming that electrons in chemical bonds are shared equally between atoms. On the other hand, the oxidation number is the number of electrons an atom loses, gains, or shares with another atom. For example, the formal charge of the nitrogen atom in the ammonia molecule is 0. However, the oxidation number is +3.