Magnesium
What is Magnesium
A silver-white tough metal, magnesium (pronounced as mag-NEE-zhi-eem) belongs to the family of alkali earth metals. Represented by the chemical symbol Mg, it burns easily in air with a distinctive bright white light [1, 2]. The eighth most abundant element in the earth’s crust, magnesium has 15 isotopes with mass numbers ranging from 20 to 34 of which only Mg-24, Mg-25, and Mg-26 occur naturally [4].
Where is Magnesium Found
It exists in a combined state as minerals like dolomite, magnesite, and carnallite. However, the main source of the metal from which 85,000 tons gets extracted every year is seawater that contains 1.3 billion kilograms of it in every cubic kilometer [1].
History
Origin of its name: It is derived from Magnesia, a district in Greece called Eastern Thessaly [1]
Who discovered it first: Joseph Black
Year and Date of discovery: 1755
When, Where, and How was it Discovered
In 1755, while heating magnesite and limestone Black identified a new element extracted from the former. Again in 1789, a Welsh surgeon called Thomas Henry identified a mineral containing the newly discovered element, suspecting its earlier use in Turkey for making tobacco pipes.
In 1792, an impure form of the element was produced by Anton Rupprecht by heating magnesia with charcoal. However, its complete isolation was carried out by the British chemist Humphry Davy in 1808 through electrolysis of magnesium oxide. It was only in 1831 when a considerable amount of the new metal was prepared and obtained by a French scientist called Antoine- Alexandre-Brutus Bussy [1].
Identification | |||||||
| Atomic number | 12 [1] | ||||||
| CAS number | 7439-95-4 [1] | ||||||
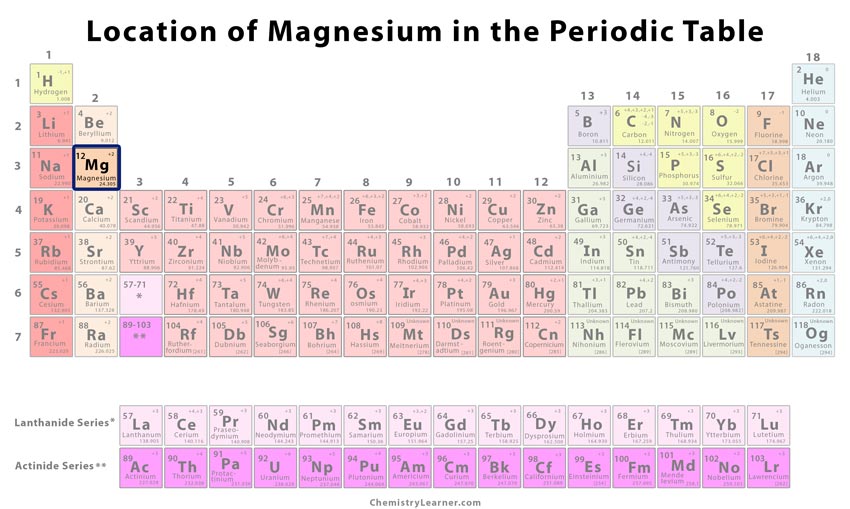
| Position in the periodic table [1] | Group | Period | Block | ||||
| 2 | 3 | s | |||||
Classification, Properties and Characteristics of Magnesium
General Properties | |||
| Relative atomic mass | 24.305 [1] | ||
| Atomic mass/weight | 24.305 atomic mass units [6] | ||
| Molar mass/Molecular weight | 24.305 g/mole [5] | ||
| Mass Number | 24 | ||
Physical Properties | |||
| Color/physical appearance | Silver white [1] | ||
| Melting point/freezing point | 650°C (1202°F) [1] | ||
| Boiling point | 1090°C (1994°F) [1] | ||
| Density | 1.74 g/cm3 [1] | ||
| Standard/Natural state at room temperature (solid/liquid/gas) | Solid [1] | ||
| Malleability | Yes | ||
| Ductility | Yes (low ductility) | ||
| Hardness | 2.5 Mohs [6] | ||
| Specific heat capacity | 1.02 J g-1 K-1 [4] | ||
| Thermal conductivity | 156 Wm-1K-1 [4] | ||
| Electrical conductivity | 22.4 x 106 Sm-1 [4] | ||
Chemical Properties | |||
| Flammability | Flammable [3] | ||
| Oxidation state/Oxidation number (numbers) | (+1), +2 [1] | ||
Atomic Data of Magnesium (Element 12)
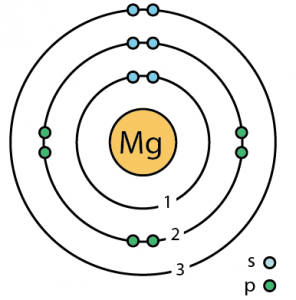
| Valence electrons | 2 [7] | ||||||
| Electron configuration (noble gas configuration) | [Ne] 3s2[1] | ||||||
| Atomic structure [4] | |||||||
| – Number of Electrons | 12 | ||||||
| – Number of Neutrons | 12 | ||||||
| – Number of Protons | 12 | ||||||
| Radius of atom | |||||||
| – Atomic Radius | 1.73 Å [1] | ||||||
| – Covalent Radius | 1.40 Å [1] | ||||||
| Ion charge | +2 | ||||||
| Ionization energy [1]
(kJmol-1) |
1st | 2nd | 3rd | 4th | 5th | 6th | 7th |
| 737.75 | 1450.683 | 7732.692 | 10542.519 | 13630.48 | 18019.6 | 21711.13 | |
What is Magnesium Commonly Used for
- Since Mg is lightweight, it is used in the making of luggage bags, car seats, laptops, power tools, and camera [1].
- As the metal is almost 1/3rd lighter than aluminum, its alloyed with the latter and used in the construction of airplanes, missiles, and cars [1, 3].
- Its ability to burn with a dazzling flame in air contributes to the sparking effect of fireworks, incendiary bombs, sparklers, and flares [1].
- Magnesium is used in removing sulfur impurities from steel and molten iron [1].
- It is a common additive in cast iron and conductive propellants [1].
What are the Toxic Effects of Magnesium Element
Inhalation of magnesium powder can be damaging to the throat, lungs, and eyes. The effects are more dangerous with higher levels, affecting the muscles and nerves [8].
Interesting Facts
- The tart flavor of mineral water is a result of addition of magnesium [9].
- It is present in chlorophyll of plants as well as in the bones of humans [1]. In fact, the image used for Mg is a representation of chlorophyll.
Magnesium Price
The cost of pure magnesium is estimated to be somewhere between $3 and $4 per 100 grams.
References
- http://www.rsc.org/periodic-table/element/12/magnesium
- https://education.jlab.org/itselemental/ele012.html
- https://www.radiochemistry.org/periodictable/elements/12.html
- https://www.chemicool.com/elements/magnesium.html
- https://pubchem.ncbi.nlm.nih.gov/compound/magnesium#section=Top
- http://periodictable.com/Properties/A/MohsHardness.al.html
- https://www.toppr.com/ask/content/story/anomalous-properties-of-fluorine-75571/
- http://www.chemistryexplained.com/elements/L-P/Magnesium.html
- https://www.thoughtco.com/interesting-magnesium-element-facts-603362